Способы резервирования в системах электроснабжения.

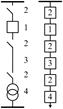Простейшей системой с точки зрения надежности является такой комплект элементов, при котором отказ одного элемента вызывает отказ всей системы, но не изменяет надежность других элементов. Такая структура называется системой с последовательным соединением элементов без резервирования.

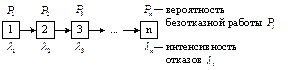
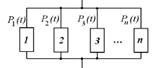Вероятность безотказной работы системы с последовательным соединением элементов определяется как вероятность безотказной работы всех элементов в течении времени t: P_с(t) = P₁(t)P₂(t)…P_n(t).

При экспоненциальном законе распределения каждого элемента вероятность безотказной работы системы из последовательно соединенных элементов также подчиняется экспоненциальному закону.

P_с(t) = e^{– λ1t} e^{– λ2t}…e^{– λnt} = e^{– Σλt}. Отсюда интенсивность отказов системы λ_с = λ₁+λ₂+…+ λ_n.

Структурой из последовательно соединенных элементов можно моделировать надежность электрических цепей с последовательным соединением аппаратов, транзисторов, проводов, кабелей и воздушных линий электропередачи, а также схем, содержащих обмотки и контакты реле, резисторы, тиристоры, катушки индуктивности и электронные приборы.

Параллельншое соединение линий, конденсаторов с инди­видуальными предохра­нителями, а также параллельная работа нескольких агрегатов (генераторы, насосы, вентиляторы и т. п. ) моделируются структурой с парал­лельным соединением элементов. Таковой можно считать систему из n элементов или единиц оборудования, если для нормальной работы необходимо r < n элементов, т. е. n – r элементов являются резервными. Отказ системы наступает при выходе из строя m элементов. Пока число резервных элементов хотя бы на один превышает число отказавших элементов, система не отказывает. Таким образом, условия отказа: m – 1 = n – r.

Следовательно, вероятность отказа системы определяется как вероятность совпадения отказов (n – r +1) или m элементов в течение расчётного периода времени.

Условие взаимонезависимости отказов элементов выполняется в том случае, если при изменении числа находящихся в работе элементов не наблюдается их значительной перегрузки. Таким образом, система с параллельным соединением элементов является резервированной системой, т.е. отказ одного или нескольких элементов не вызывает отказа всей системы.

В теории надежности различают два способа резервирования:

1. Постоянное – резервирование, при котором в работе постоянно находятся все элементы, и система не отказывает до выхода из строя определенного их числа.

2. Замещением – резервирование, при котором резервные элементы включаются только после автоматического отключения отказавших элементов.

В энергетике резервирование замещением осуществляется многочисленными устройствами АВР («холодный» резерв), постоянное – вращающимся и скрытым резервом генераторов, трансформаторов и электродвигателей («горячий» резерв).

При постоянном резервировании важнейшим показателем надежности является кратность резервирования – соотношение числа рабочих и резервных элементов:

k = (n – r)/r = (m – 1)/(n – m + 1).

Для различных k существуют таблицы и кривые зависимости вероятности безотказной работы системы от кратности резервирования при экспоненциальном законе

P_k(t) = f(k,t)

Резервирование с дробной кратностью (k < 1 ) повышает вероятность безотказной работы только при малых значениях мат.ожидания числа отказов.

Вероятность безотказной работы системы с резервированием определяется надежностью не только самих элементов, но и систем автоматики, которые при постоянном резервировании должны отключать отказавший элемент, а при резервировании замещением – еще и включать резервный.

Зачастую выбор объекта для резервирования может быть многозначным. Примерами такого резервирования могут являться замещение данного объекта одним из резервных, различным по своим свойствам, различным по стоимости, по техническим характеристикам.

Мажорантным (или мажоритарным) с точки зрения надежности является тип резервирования, при котором выбор резервного объекта осуществляется исходя из наибольшей надежности включаемого резервного элемента. Естественно, число резервных элементов должно быть не менее двух, они должны отличаться по своим показателям надежности.

Минорантным (или миноритарным) резервирование с точки зрения надежности является резервирование, при котором выбор резервного элемента из ряда замещающих осуществляется не по критерию наибольшей надежности, а какому-либо другому критерию (экономическому).

Приоритетные виды резервирования применяются только там и тогда, где и когда различные показатели резервных элементов действительно имеют технический и экономический смысл и могут быть реализованы системами автоматического включения резерва.

26. Расчеты вероятностей отказа и безотказной работы при различных видах резервирования.

Вероятность безотказной работы системы с последовательным соединением элементов без резервирования определяется как вероятность безотказной работы всех элементов в течении времени t:

P_с(t) = P₁(t)P₂(t)…P_n(t), где P_i(t) – вероятность безотказной работы i-го элемента.

При экспоненциальном законе распределения каждого элемента вероятность безотказной работы системы из последовательно соединенных элементов также подчиняется экспоненциальному закону.

P_с(t) = e^{– λ1t} e^{– λ2t}…e^{– λnt} = e^{– Σλt}. Отсюда интенсивность отказов системы λ_с = λ₁+λ₂+…+ λ_n.

Вероятность отказа системы по определению Q_с(t) = Q₁(t)+Q₂(t)+…+Q_n(t).

В теории надежности различают два способа резервирования:

1. Постоянное – резервирование, при котором в работе постоянно находятся все элементы, и система не отказывает до выхода из строя определенного их числа.

2. Замещением – резервирование, при котором резервные элементы включаются только после автоматического отключения отказавших элементов.

При постоянном резервировании важнейшим показателем надежности является кратность резервирования – соотношение числа рабочих и резервных элементов:

k = (n – r)/r = (m – 1)/(n – m + 1),

где n – общее число элементов системы, работающих параллельно, r – число элементов, необходимых для нормальной работы (r < n), (n – r) – число резервных элементов, m – число элементов, отказ которого приводит к выходу системы из строя.

Таким образом, условие отказа: m – 1 = n – r.

Если отказы одного элемента независимы от отказов других элементов, то формулы для оценки вероятности безотказной работы и вероятности отказа системы можно получить, сформировав сумму произведения вероятностей Q_i(t) и P_i(t) на основе произведения n биномов

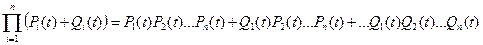
Выбрав из этой суммы члены с числом элементов Q_i(t), большим или равным m, можно сформировать из них выражение для вероятности отказа. Выбрав же члены с числом Q_i(t), меньшим m, можно сформировать из них выражение для вероятности безотказной работы системы с параллельным соединением элементов.

При условии равной надежности элементов

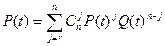; , где .

Для различных k существуют таблицы и кривые зависимости вероятности безотказной работы системы от кратности резервирования при экспоненциальном законе

P_k(t) = f(k,t)

Вероятность безотказной работы системы с резервированием определяется надежностью не только самих элементов, но и систем автоматики, которые при постоянном резервировании должны отключать отказавший элемент, а при резервировании замещением – еще и включать резервный.

Если при отказе отключающей аппаратуры в отключении выводится вся система, то вероятность безотказной работы системы с постоянным резервированием: P_с(t) = P_k(t)P_А(t),

где P_k – вероятность безотказной работы группы элементов с кратностно резервированным k; P_А – вероятность отсутствия отказов срабатывания при отключении отказавших элементов.

При резервировании замещением вероятность отказа системы определяется по формуле полной вероятности:

Q_с = 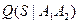P(A₁)P(A₂) + 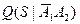Q(A₁)P(A₂) + 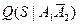P(A₁)Q(A₂) + 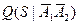Q(A₁)Q(A₂)

где 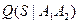– условная вероятность отказа системы при отсутствии отказов отключающей и включающей аппаратуры;

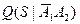– условная вероятность отказа системы при отказе в отключении отказавшего элемента;

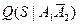– условная вероятность отказа системы при отказе во включении резервного элемента;

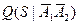– условная вероятность отказа системы при совпадении отказа в отключении отказавшего и включении резервного элементов;

P(A₁), Q(A₁) – вероятность соответственно отсутствия отказа и отказа в отключении отказавшего элемента;

P(A₂), Q(A₂) – вероятность соответственно отсутствия отказа и отказа во включении резервного элемента.