Линейные электрические цепи постоянного тока

1. Вначале необходимо повторить из курса физики определение электрических величин: ЭДС, напряжения, потенциала, разности потенциалов, тока, сопротивления.

2. Следует усвоить основные законы цепей постоянного тока: Ома, Кирхгофа, Джоуля – Ленца. За положительное направление напряжения принято направление, совпадающее с выбранным положительным направлением тока, т.е. от точки a с большим потенциалом к точке b с меньшим потенциалом. (Рис. 2.1)

Рис. 2.1

Направление ЭДС характеризует способность стороннего поля вызывать электрический ток, в источнике направлено от электрода b c отрицательным потенциалом «−» к электроду с положительным «+» потенциалом с, т.е. обратно напряжению источника U_cb (рис. 2.2).

Рис. 2.2

3. Законы Кирхгофа – основные законы электротехники.

Первый закон Кирхгофа применяется к узлам электрической цепи: алгебраическая сумма токов в узле равна нулю, т.е. , где n – число ветвей, соединенных в данном узле. Знаки токов берут произвольно, например, токи, направленные к узлу – со знаком плюс, тогда от узла – со знаком минус (или наоборот).

Второй закон Кирхгофа применяется к контурам электрической цепи: алгебраическая сумма ЭДС в этом контуре равна алгебраической сумме напряжений в этом контуре, т.е. , где m – число ЭДС в контуре; p – число напряжений U_К=I_КR_К в контуре. ЭДС и напряжения берут со знаком плюс, если их направление совпадает с принятым направлением обхода контура. Обход контура принимается произвольно, но для удобства расчетов для всех контуров рекомендуется выбирать одинаковым.

4. Законы Джоуля – Ленца: энергия W источника и приемника соответственно равны: , где Е – ЭДС источника; U – напряжение приемника; t – время; I – ток. Их мощности: P_И= W_И / t = E I и P_П=W_П / t = U I = I² R = U² / R. Если E и I имеют разные знаки, то мощность источника отрицательна, т.е. он не вырабатывает энергию, а её потребляет. То же самое правило применяется при составлении баланса мощностей для цепи.

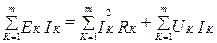, где E_К и U_К – ЭДС и напряжение источников энергии.

5. Потенциальной диаграммой называется график V(R) распределения потенциала в цепи в функции сопротивления участков цепи.

Для построения потенциальной диаграммы предварительно должны быть рассчитаны токи на участках рассматриваемого контура. Потенциал одной из точек цепи, принимают равным нулю V=0, рассчитывают потенциалы остальных точек, учитывая, что потенциалы соседних точек увеличиваются, если расчет ведется против направления тока и наоборот. На участке с источником ЭДС происходит скачок потенциала.

6. Сложные электрические цепи с одним источником ЭДС во многих случаях целесообразно решать методом эквивалентных преобразований, т.е. упрощением их путем свертывания, заменяя отдельные участки цепи с последовательным, параллельным и смешанным соединениями сопротивлений одним эквивалентным сопротивлением.

Участок электрической цепи (цепь) с последовательным соединением сопротивлений заменяется при этом цепью с одним эквивалентным сопротивлением , где R_K – сопротивление K – го участка цепи.

Электрическая цепь, состоящая из n параллельно соединенных сопротивлений заменяется эквивалентным сопротивлением .

Эквивалентное сопротивление при смешанном (последовательном и параллельном) соединении сопротивлений определяется .

7. Основным методом расчета разветвленных электрических цепей с несколькими источниками питания является метод непосредственного применения законов Кирхгофа.

Пусть цепь содержит m ветвей и n узлов. Так как по каждой ветви проходит свой ток, то число неизвестных токов равно числу ветвей и для их определения необходимо составить m уравнений.

Последовательность расчета:

а) обозначают стрелками токи во всех m ветвях, произвольно выбрав их направления;

б) составляют по первому закону Кирхгофа уравнения для (n − 1) узлов;

в) недостающие m – (n − 1) уравнения составляют по второму закону Кирхгофа, для взаимно независимых контуров (последующий контур содержит новую ветвь). Выбирают направления обхода контуров.

В результате решения этой системы уравнений определяются как числовые значения токов, так и их действительные направления. Если ток получился с отрицательным знаком, то его действительное направление противоположно выбранному.

8. На основании методов законов Кирхгофа разработан ряд методов расчета (контурных токов, двух узлов, наложения, эквивалентного генератора), позволяющих в частных случаях упростить расчет сложной цепи. Так, метод контурных токов является более универсальным, позволяет сократить число совместно решаемых уравнений с m до m – (n – 1).

Последовательность расчета:

а) выбирают в схеме взаимно независимые контуры;

б) для выбранных независимых контуров принимают произвольно направления контурных токов;

в) составляют для выбранных контуров уравнения по второму закону Кирхгофа относительно контурных токов.

г) по найденным контурным токам определяют действительные токи в ветвях. Учитывая, что в крайних ветвях они равны контурным токам, а в смежных алгебраической сумме соответствующих контурных токов.

Литература [1] §1.1 – 1.5, 1.7 – 1.9, 1.11, 1.15; [3] § 1.3 – 1.5, 1.8 – 1.12.

Пример: Электрическая цепь постоянного тока содержит: источники питания Е₁ = 100 В, Е₂ = 120 В, которые имеют внутренние сопротивления R₀₁ = R₀₂ = 0,5 Ом, резисторы с сопротивлениями R₁=5 Ом, R₂ = 10 Ом, R₃ = 2 Ом, R₄ = 10 Ом. Необходимо выполнить следующее:

1) составить системы уравнений по законам Кирхгофа;

2) найти все токи, пользуясь методом контурных токов;

3) определить показания вольтметра и составить баланс мощностей;

4) построить в масштабе потенциальную диаграмму для внешнего контура.

Рис. 2.3

Решение:

1. Составим систему уравнений по законам Кирхгофа. Схема содержит 6 ветвей и 4 узла (m=6, n=4).

Произвольно выбираем положительные направления всех шести токов (рис. 2.3).

По первому закону Кирхгофа составляем 4–1=3 уравнения для узлов a, b, c.

I₁+ I₂ + I₃ = 0

I₅ – I₁ – I₄ = 0

I₄ – I₂ – I₆ =0

Приняв направление обхода контуров по часовой стрелке, составим m–(n–1)=6 – 3 =3 уравнения для взаимно независимых контуров по второму закону Кирхгофа:

контур adba E₁ = R₁ I₁ – R₃ I₃ + R₀₁ I₅;

контур bacdb E₁ – E₂ = R₁ I₁ – R₂ I₂ + R₀₂ I₆ + R₀₁ I₅ ;

контур bcab R₄ I₄ + R₂ I₂ – R₁ I₁ = 0.

2. Находим токи методом контурных токов. Произвольно задается направление контурных токов, например, по часовой стрелке (рис. 2.4). Обходя по часовой стрелке, составляем уравнение для трех контуров.

Рис. 2.4

Первый контур E₁ = (R₁ + R₃ + R₀₁) I_I – R₁ I_III – R₃ I_II .

Второй контур – E₂ = (R₂ + R₀₂ + R₃) I_II – R₃ I_I – R₂ I_III .

Третий контур 0 = (R₁ + R₄ + R₂) I_III – R₁ I_I – R₂ I_II .

Подставив численные значения, решаем.

100 = 7,5 I_I – 2 I_II – 5 I_III

−120 = −2 I_I + 12,5 I_II –10 I_III

0 = −5 I_I −10 I_II + 25 I_III

Решая методом подстановок, получим:

I_I = 9, 43 А;

I_II = −9,68 А;

I_III = −1, 99 А.

Определяем действительные токи ветвей, учитывая ранее принятые направления токов (рис. 2.3).

I₁ = I_I – I_III = 9,43 – ( −1,99) = 11,42 А;

I₂ = I_III – I_II = −1,99 – (−9,68) = 7,96 А;

I₃ = I_II – I_I = −9,68 – 9,43 = −19,11 А;

I₄ = I_III = −1,99 А; I₅ = I_I = 9,43 А; I₆ = I_II = −9,68 А.

У токов I₃ I₄ и I₆ действительное направление противоположно выбранному, что отмечается крестиком на конце стрелки указателя направления соответствующего тока (рис. 2.4).

3. Определяем показания вольтметра и проверяем правильность решения задачи балансом мощностей.

Для определения показания вольтметра для контура acka, включая вольтметр (рис. 2.4) составляем уравнение по второму закону Кирхгофа, приняв обход по часовой стрелке и потенциал V_K > V_a

−E₂ = −R₂ I₂ +R ₀₂ I₆ + U_Ka , откуда

V_K2 = R₂ I₂ – R ₀₂ I₆ – E₂ = 10 • 7,69 + 0,5 • 9,68 – 120 = −38,26 В. Отрицательный знак напряжения вольтметра показывает, что в действительности потенциал V_K < V_a..

Составляем уравнение баланса мощностей всей цепи:

, где ЕI и UI, соответственно, мощности источников ЭДС и напряжения. Стрелками указаны фактические направления ЭДС, U и I.

E₁ I₅ + E₂ I₆ = I²₁ R₁ +I²₂R₂+ I²₃R₃ + I²₄ R₄ + I²₅ R₀₁ + I²₆ R₀₂

100 • 9,43 + 120 • 9,68 = 11,42² • 5 + 7,69² • 10 +19,11² • 2 + 1,99² • 10 + 9,43² •0,5 + 9,68² • 0,5 = 2104,6 ≈ 2104,7 Вт,

100 • 9,43 + 120 • 9,68 = 11,42² • 5 + 7,69² • 10 +19,11² • 2 + 1,99² • 10 + 9,43² •0,5 + 9,68² • 0,5 = 2104,6 ≈ 2104,7 Вт, т.е. в пределах требуемой точности соблюдается баланс мощности и расчет сделан верно.

4. Потенциальную диаграмму строим для внешнего контура bcdefb (рис. 2.5). На рис. 2.5 также указаны внутренние сопротивления источников R₀₁ и R₀₂ и показаны действительные направления токов. Потенциал точки b принимаем равным нулю (V_b = 0). Двигаясь против тока I₄ имеем: V_c – V_b = R₄ I₄, откуда

V_c = R₄ I₄ + V_b = 10 • 1,99 + 0 = 19,9 B

V_e = R₀₂ I₆ + V_c = 0,5 • 9,68 + 19,9 = 24,74

V_d = V_e – E₂ = 27,74 – 120 = - 95,26 B

V_f = V_d + E₁ = - 95,26 + 100 = 4,74 B

V_b = V_f – R₀₁ • I₅ = 4,74 – 0,5 • 9,43 = 4,74 – 4,715 ≈ 0.

Рис. 2.5

Строим потенциальную диаграмму V (R) (Рис. 2.6)

Рис. 2.6

Вопросы для самопроверки

1. Напишите закон Ома для участка цепи.

2. Напишите обобщенный закон Ома для всей цепи (для активного участка).

3. Сформулируйте законы Кирхгофа и напишите их математические выражения.

4. Выведите выражения для эквивалентного сопротивления участка цепи, состоящего из n последовательно соединенных сопротивлений.

5. Выведите выражение для эквивалентного сопротивления участка цепи, состоящего из n (n = 2, n = 3, n=k) параллельно соединенных сопротивлений.

6. Напишите выражение баланса мощности для цепи с несколькими источниками питания и несколькими резисторами.

7. Изложите сущность метода контурных токов.

8. Когда можно воспользоваться методом узлового напряжения?

9. Назначение потенциальной диаграммы.

10. Назначение потенциальной диаграммы.