Электрические цепи однофазного переменного тока

1. В однофазных электрических цепях в большинстве случаев действует ЭДС, изменяющиеся по синусоидальному закону, поэтому в линейных однофазных цепях токи и напряжения также синусоидальны.

2. Мгновенное значение синусоидально изменяющейся величины а можно выразить аналитически: a = A_m Sin (ωt + ψ_а), где A_m - амплитудное значение, ω – угловая частота, ψ_а – начальная фаза. Аналогично для ЭДС e=E_mSin(ωt + ψ_е), напряжения u=U_mSin(ωt + ψ_u).

Известно, что синусоидально изменяющаяся величина может быть условно (символически) представлена в виде комплексного числа A (E, U, I), которое записывается в трех формах: показательной A = Ae^jψа = A (cos ψ_а+ jsinψ_а) = A'+ jA",тригонометрический A=A(сosψ_а+jsinψ_а) и алгебраический A=A'+jA". Здесь - действующее значение синусоидальной величины; ψ_а – начальная фаза; A' и j A" – действующая и мнимая составляющие комплексного числа. Такие же выражения при необходимости можно записать для амплитудных величин.

Переход от показательной к алгебраической форме записи выполняется по формулам: A'=Аcosψ_а; A"=Аsinψ_а, а обратный переход при A' > 0 и +180° приA' < 0.

Комплексные числа можно также представить как векторы на комплексной плоскости. Алгебраические действия над синусоидальными величинами можно заменить действиями над комплексными величинами или над векторами. Поэтому алгебра комплексных чисел является основным математическим аппаратом при расчете цепей однофазного синусоидального тока, а векторная алгебра – наглядным средством изображения синусоидально изменяющихся величин.

3. При расчете цепей синусоидального тока, в отличие от расчета цепей постоянного тока, необходимо учитывать не один, а три пассивных элемента: резистивный, индуктивный и емкостной, которые характеризуются соответственно активным сопротивлением R, индуктивностью L (индуктивным сопротивлением X_L=ωL), и емкостью С (емкостным сопротивлением Х_С=1/ωС), где ω – угловая частота.

Индуктивное X_L и емкостное Х_С сопротивления определяют не только значения токов в цепи, но также сдвиг фаз φ между напряжениями и токами. Так, в цепи с активным сопротивлением напряжение и ток по фазе совпадают φ = 0, с индуктивностью ток отстаёт на φ = 90 °, а в цепи с ёмкостью – ток опережает напряжение на φ = 90 °.

При включении в цепь индуктивности L часто говорят об индуктивном сопротивлении, индуктивном падении напряжения или индуктивной составляющей напряжения. Однако в действительности в этих понятиях есть условность. При включении в цепь реальной катушки, обладающей активным сопротивлением R и индуктивностью L, на переменное синусоидальное напряжение уравнение по второму закону Кирхгофа записывается в виде: u=Ri+(−e_L). Это объясняется тем, что часть напряжения u падает в сопротивлении R (т.е. Ri), а остальная часть расходуется на компенсацию возникающей ЭДС самоиндукции (е_L). Численно же величина действующей ЭДС E_L=−ωLI. Так как ωL = Х_L и выражается в Омах, то его называют реактивным индуктивным сопротивлением, а произведение Х_LI – индуктивным падением напряжения (по аналогии с произведением RI). Аналогично Х_С=1/ωС называют емкостным сопротивлением, а Х_СI – емкостным падением напряжения.

4. При расчете цепей синусоидального тока все законы и методы расчета цепей постоянного тока действительны в комплексной форме. При этом следует иметь в виду, что действительная и мнимая части комплексного сопротивления (Z=R ± jX), комплексной проводимости (Y = G ± j B) и комплексной мощности (S=P±jQ) всегда представляет собой соответственно активную (R, G, P) и реактивную (X,B,Q) составляющую этих величин. Действительная и мнимая части комплексного напряжения и комплексного тока определяются начальными фазами величин, т.е. зависят от расположения соответствующих векторов относительно осей комплексной плоскости, тогда как их активная и реактивная составляющая определяются углом сдвига фаз j между этими двумя векторами.

5. Расчет цепей синусоидального тока может быть выполнен и без применения комплексных чисел (алгебраический метод). Основные расчетные формулы при этом следующие:

при последовательном соединении элементов R, L, C:

- полное сопротивление,

I = U / Z – закон Ома,

j = arc tg (X_L - X_C) / R – угол сдвига фаз,

Х – реактивное сопротивление цепи.

При параллельном соединении двух ветвей с элементами R₁, L в одной ветви и R₂, C – в другой:

- полная проводимость, где G₁=R₁ / (R₁² + X_L²), G₂ = R₂ / (R₂² + X_C²), G – активная проводимость ветвей и цепи; B_L = X_L/(R₁² + X_L²), B_C=X_C /(R₂²+ X_C²), B – реактивные проводимости ветвей и цепи.

Следует обратить внимание на то, что понятия активной и реактивной проводимости имеют условно-расчетный характер. Как видно из приведенных выше выражений этих проводимостей, они включают в себя как активные R₁, R₂ так и реактивные X_L, X_C сопротивления.

6. При резонансе напряжение и ток в общей части цепи всегда совпадают по фазе (j = 0). Для последовательной цепи условием резонанса является равенство индуктивного и емкостного сопротивлений: X_L и X_C. Для параллельной – равенство реактивных проводимостей: В_L и В_C.

При резонансе напряжений (последовательное соединение R, L и С элементов) резонансная частота , цепь носит активный характер (j = 0), полное сопротивление равно активному и минимально, ток в цепи I=U/R максимальный, напряжение на реактивных элементах цепи при R<X_L = X_C больше, чем напряжение, подведенное к зажимам цепи, (что представляет повышенную электроопасность), потребляемая цепью активная мощность P=RI² максимальна и равна полной S = P.

При резонансе токов (параллельное соединение элементов R₁, L и R₂, C) резонансная частота и зависит как от параметров L, C, так и от активных сопротивлений R₁, R₂. Цепь носит активный характер (j=0), полная проводимость равна сумме активных проводимостей ветвей и минимальна, ток в общей части цепи I = YU = GU = I_R минимален и равен активной составляющей, реактивные составляющие тока в ветвях равны (I_L = I_C), при G < B_L = B_C они больше, чем ток в общей части цепи, реактивные мощности элементов L и С равны Q_L = Q_C = B_L U² = B_C U², полная мощность S =UI =UI_R = P минимальна и равна активной мощности Р.

7. Резонанс напряжений (X_L = X_C или ) можно получить либо изменением индуктивности L, либо емкости С или частоты f переменного тока источника.

8. Для расчета разветвленных цепей рекомендуется применять комплексный метод. Для цепей с одним источником питания можно использовать метод эквивалентного преобразования, для цепей с несколькими источниками питания – любые методы для цепей постоянного тока, но записывать их в комплексной форме, т.е. вместо тока I, напряжения U, ЭДС Е, сопротивления R следует записывать их комплексные значения I, U, E, Z.

Литература [1] § 2.1 – 2.4, 2.6 – 2.22; [3] §2.1-2.11; [4] §2.1 – 2.18.

Пример: рассчитать электрическую цепь синусоидального тока со смешанным соединением приемников (рис. 2.7).

Рис. 2.7

Дано: U = 120В, R₁ = 10 Ом, R₂=24 Ом, R₃=15 Ом, L₁=19,1 мГ, C₂ = 455 мкФ, L₃ = 63,5 мГ, f = 50 Гц. Определить токи на участках цепи, напряжения на участках цепи U_ab, U_bc , активную, реактивную и полную мощности и построить векторную и потенциальную диаграмму на комплексной плоскости.

Решение: выражаем сопротивления ветвей цепи в комплексной форме:

Z = R ± j X = Z e ^{± j j} ;

Z₁ = R₁+jwL₁ = 10 + j2pּ50 ּ19,1 ּ10^-3 = 10 + j6 Ом

Переходя от алгебраической формы записи комплексного числа к показательной, получаем: Ом, где 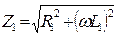= , tgφ₁= , ,

.

Полное комплексное сопротивление цепи:

== 24,4 + j10,8 = 26,7 e ^{j 23˚ 55’} Oм.

Выражаем заданное напряжение U в комплексной форме. Для удобства принимаем вектор напряжения совпадающим с положительным направлением действительной оси, тогда:

U = U + j O = U = 120 B.

Определяем ток в неразветвленной части цепи I₁:

I₁ = U / Z = 120 / 26,7 e ^{j 23˚ 55´} = 4,11 – j1,82 A = 4,5е^{-J 23º 55´}

Падение напряжения на участках цепи U_ab и U_bc:

U _ab = Z₁ I₁ = 11,6 e ^{j 31˚ ּ} 4,5 e ^{–j 23°55´} = 52,2 ^{j 7º 55´} B =51,8 + j6,4 B

= 68,4 e^{-j 5º30’} B = 68,1 – j6,6 B или U_bc = U - U_ab

Находим токи параллельных ветвей I₂, I₃:

I₂ = U_bc / Z₂ = 68,4 e ^{– j 5º30’} / 25 e ^{– j 16º 15’} = 2,74 e ^{j 10º45’} A =2,7 + j0,51 A;

I₃ = U_bc / Z₃ = 68,4 e ^{– j 5º30´} / 25 e ^{j 53º 05´}= 2,74 e ^{-j 58º35´} A =1,4 – j2,3 A.

Находим мощности всей цепи и отдельно её ветвей

S = UI₁^* = P ± jQ, где I₁^* - комплексный сопряженный ток, у которого знак при мнимой слагаемой противоположный.

S = 120ּ(4.11 + j 1,82) = 493 + 218 BּA, где Р = 493 Вт – активная мощность цепи; Q = 218 вар – реактивная индуктивная мощность цепи.

Проведем проверку балансом мощностей:

P = P₁ + P₂ + P₃ = R₁I₁² + R₂I₂² + R₃I₃² = 10ּ4,5² + 24ּ2,74² + 15ּ2,74² = 493 Bт.

Учитывая, что Q₁ и Q₃ положительны (реактивная мощность индуктивных катушек), а Q₂ отрицательна (реактивная мощность конденсатора) получим:

Q = Q₁ – Q₂ + Q₃ = X₁I₁² – X₂I₂² + X₃I₃² = 6ּ4,5² − 7ּ2,74² + 20ּ2,74² =

= 218 вар.

На рис. 2.8 приведена векторная диаграмма токов и напряжений.

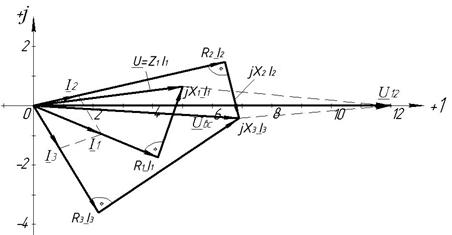
Рис. 2.8

Порядок её построения следующий: принимаем масштабы токов М_I = 2А/см и напряжений М_U = 10 В/см, по результатам расчетов отложены векторы токов I₁, I₂, I₃, затем по направлению I₁ отложен вектор R₁I₁ и перпендикулярно к нему в сторону опережения (против часовой стрелки) вектор jX₁I₁. Их сумма дает вектор Z₁I₁ = U.

V_R1 = R₁I₁ = 10 (4,11- j 1,82) = 41,1 – j18,2 B = 45 e ^{–j 23º55’} B

U_X1 = jX₁I₁ = j6 (4,11 – j 1,82) = 7,5 + j 24,7 B = 25,8 e ^{j 73º06’} B

U_R2 = R₂I₂ = 24ּ2,74 e ^{j 10º45’} = 65,76 e ^j10º45’ B

U_X2 = - jX₂I₂ = - j 7ּ2,74 e ^{j 10º45’} = - j7 (2,7 + j 0,51) = 3,57 – j18,9 B =

=19,2 e ^{-j 79º18’} B

U_R3 = R₃I₃ = 15ּ2,74 e ^{-j 58º35’} = 41,1 e ^{–j58º35’} B

U_X3 = jX₃I₃ = j20(1,4 – j2,3) = 46 + j28 B = 53,85 e ^{j 31º20’}B

Далее в фазе с I₂ строится вектор R₂I₂ и перпендикулярно к нему в сторону отставания вектор jX₂I₂, а их сумма дает вектор напряжения на параллельном участке U_bc. Тот же вектор можно получить, если в фазе с I₃ отложить R₃I₃ и к нему прибавить вектор jX₃I₃, опережающий I₃ на 90º. Сумма векторов Z₁I₁ и U_bc дает вектор приложенного напряжения U.

Потенциальная типографическая диаграмма рассчитывается по тому же методу, что и в цепях постоянного тока. В соответствии с положительным направлением токов потенциал точки с примем равным 0 (V_c = 0).

Комплексные потенциалы точек К и N

V_k = V_c + jX₂I₂ = 0 + 19,2 e ^{– j 79º18’} = 19,2 e^{– j 79º18’}B

V_n = V_c + jX₃I₃ = 0 + 53,85 e ^{j 31º20’} = 53,85 e ^{j 31º20’} B

Потенциал точки b

V_b = V_c + U _bc = 0 + 68,4 e ^{-j 5º30’} = 68,4 ^-e ^{j 5º30’} B = 68,1 – j6,6 B

Потенциал точки m

V_m = V_b + jX₁I₁ = 68,1 – j6,6 + 7,5 + j 24,7 = 75,6 + j18,1 = 77,74 e ^j13º28’ B

Потенциал точки a

V_a = V_m + R₁I₁ = 75,6 + j18,1 + 41,1 – j18,2 » 120B

Отложив на комплексной плоскости векторы токов (рис. 2.9) I₁, I₂, I₃ и комплексных потенциалов V_k, V_n, V_b, V_m, V_a, получим на диаграмме точки a, m, b, n, k. Соединяющие их векторы равны соответствующим комплексным напряжениям.

Рис. 2.9

Вопросы для самопроверки

1. Какими величинами определяется синусоидально изменяющаяся функция?

2. Дайте определение действующих значений синусоидального тока. Запишите соотношение между амплитудным и действующим значениями тока, напряжения, ЭДС.

3. Как зависят индуктивные и емкостные сопротивления от частоты?

4. От чего зависит угол сдвига фаз в электрической цепи однофазного синусоидального тока?

5. Каковы углы сдвига фаз между напряжениями R - , L - и С - элементов, включенных последовательно?

6. Каковы углы сдвига фаз между токами R - , L - и С - элементов, включенных параллельно?

7. Напишите законы Ома в комплексной форме, а также выражение эквивалентного комплексного сопротивления для последовательного, параллельного и смешанного соединения сопротивлений.

8. Какие энергетические процессы характеризуют активная и реактивная мощности?

9. Напишите условия наступления резонанса напряжений, токов. Начертите для этих режимов векторную диаграмму.

10. Почему и как стремятся повысить коэффициент мощности в электрических цепях?