
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Трансформаторы
1. Прежде всего, необходимо повторить основной закон электромагнетизма – закон электромагнитной индукции 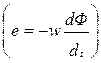
 и явления самоиндукции и взаимоиндукции, которые лежат в основе принципа работы трансформаторов.
и явления самоиндукции и взаимоиндукции, которые лежат в основе принципа работы трансформаторов.
2. Режим холостого хода для первичной обмотки трансформатора аналогичен режиму работы катушки с ферромагнитным сердечником, поэтому этот раздел также необходимо повторить.
3. Коэффициентом трансформации n называется отношение номинального высшего напряжения трансформатора к номинальному низшему напряжению, т.е. n = Uвн / Uнн = wвн/wнн, причем это напряжение на обмотках трансформатора, работающего в режиме холостого хода.
4. Под номинальной мощностью трансформатора понимают его полную мощность Sн в номинальном режиме: Sн = U1н I1н = U2н I2н.
5. Для удобства и упрощения расчетов величины вторичной обмотки приводят к числу витков первичной обмотки: U2'= nU2, I2' = I2 / n, R2' = n2R2, X2' = n2X2, Z2' = n2Z2, Zн' = n2Zн.
Трансформатор в этом случае называется приведенным, который имеет коэффициент трансформации n = 1.
6. В работе трансформатора важное значение имеет то положение, что при изменении его нагрузки от холостого хода до номинального при постоянном первичном напряжении магнитный поток можно считать практически постоянным, поскольку U1» E1 = 4,44 fw1Фm.
7. Так как Ф ≈ const, то алгебраическая сумма МДС (магнитодвижущих сил), создающих этот поток, в любом режиме одинакова, т.е.
I1X w1 = I1w1 – I2w2,
где I1X, I1 и I2, соответственно, токи холостого хода, первичной и вторичной обмоток трансформатора при нагрузке.
Всякие изменения тока I2 от нагрузки приводит к такому изменению тока I1, при котором МДС обмоток остаётся неизменной. Такое положение относится не только к трансформаторам, но также к машинам переменного тока – асинхронным и синхронным.
8. Работа приведенного трансформатора во всех режимах описывается тремя уравнениями:
уравнением электрического состояния первичной цепи:
U1 = E1 + R1I1 + jX1I2;
Уравнение электрического состояния вторичной цепи:
E2' = U2' + R2'I2' + jX2'I2';
Уравнение МДС:
I1 – I2' = I1X.
9. Для лучшего понимания принципа работы нагруженного трансформатора целесообразно использовать так называемую условно-логическую схему (рис. 2.13), которая читается следующим образом.

Рис. 2.13
К первичной обмотке подводится синусоидальное напряжение u1, под действием которого в обмотке возникает ток i1 и создается МДС i1w1 . МДС i1w1 вызывает магнитный поток Ф1 и поток рассеяния Ф1d. Магнитные потоки Ф1 и Ф2 (о потоке Ф2 будет сказано ниже) создают результирующий поток Фр, который в соответствии с законом электромагнитной индукции (ЭМИ) наводит в первичной и вторичной обмотках соответственно ЭДС самоиндукции е1 и взаимоиндукции е2. Так как вторичная обмотка замкнута (з), по ней под действием е2 протекает ток i2, создающий МДС i2w2, а последний – поток Ф2. В силу закона сохранения энергии МДС i2w2 и поток Ф2 направлены соответственно против МДС i1w1 и потока Ф1, т.е. поток вторичной обмотки тем самым постоянно стремится размагнитить трансформатор.
При изменении тока i2, например, в сторону возрастания, поток Ф2 увеличивается, магнитный поток Фр и ЭДС самоиндукции е1 уменьшается, а ток i1 увеличивается на столько, пока результирующий поток Фр не достигнет первоначального значения. Таким образом, в трансформаторе имеются две обратные связи: от тока i2 к магнитному потоку Фр и от потока Фр к ЭДС е1 и ток i1.
10. Векторная диаграмма трансформатора позволяет наглядно представить соотношения и углы сдвига фаз между различными величинами. Её строят на основании приведенных в п. 8 уравнений трансформатора, начиная с произвольной точки в произвольном направлении проведением вектора тока I2.
11. Схему замещения трансформатора (рис. 2.15) строят для приведенного трансформатора также на основании его уравнений. Подобная же схема замещения используется в теории асинхронных машин из-за существования некоторой аналогии между процессами в асинхронной машине и в трансформаторе. Схема замещения позволяет более просто и наглядно производить изучение процессов в реальной машине на электрической схеме, описываемой уравнениями одинакового вида. Они бывают Т-, Г-образные и упрощенного вида.
12. Опыты холостого хода и короткого замыкания позволяют найти потери в трансформаторе, его КПД и параметры схемы замещения.
Из опыта холостого хода находят коэффициент трансформации n = Uвн / Uнн, мощность потерь холостого хода Рх (магнитные потери ΔРм) параметры ветви холостого хода (IX = I1X, Z0 = U1н / I1X, R0 = PX / I1X2,  ).
).
Из опыта короткого замыкания находят мощность электрических потерь в номинальном режиме (Рк.н. = ΔРэ), полное сопротивление упрощенной схемы замещения Zк = U1к / I1н , активное Rк = R1 + R2' = Рк / I1н2 и реактивное Хк = Х1 + Х2'= 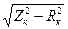 сопротивления обмоток трансформатора, напряжения короткого замыкания Uк%= (ZкI1н / U1н)100, активную Uк.а%=(RкI1н/U1н)100 и реактивную Uк.р%=(ХкI1н/U1н)100 составляющие напряжения короткого замыкания:
сопротивления обмоток трансформатора, напряжения короткого замыкания Uк%= (ZкI1н / U1н)100, активную Uк.а%=(RкI1н/U1н)100 и реактивную Uк.р%=(ХкI1н/U1н)100 составляющие напряжения короткого замыкания:

13. Изменение вторичного напряжения рассчитывают по формуле:
ΔU2 = β (Uк.а cos φ2 + Uк.р. Sin φ2) = β Uк cos (φ2 – φк),
где β = I2 / I2н = I1 / I1н – коэффициент нагрузки; φ2 – угол сдвига фаз между напряжением и током в нагрузке; φк – угол сдвига фаз в опыте короткого замыкания.
14. КПД трансформатора определяется по формуле:
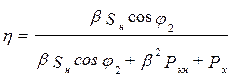
15. В трехфазных трансформаторах алгебраическая сумма мгновенных синусоидальных магнитных потоков в сердечнике равен нулю, поэтому необходимость в «нейтральном» стержне отпадает и трехфазный трансформатор выполняют в виде трехстержневого.
Под номинальными данными трехфазных трансформаторов понимают полную номинальную мощность трех фаз: 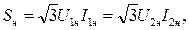 где U1н, U2н – номинальные линейные напряжения; I1н, I2н – номинальные линейные токи; мощность потерь холостого хода и короткого замыкания на три фазы Рх и Рк; номинальный КПД ηн, который задается при активной нагрузке (сos φ2 = 1) и при коэффициентах загрузки β=1 и β=0,5; группы соединений обмоток трансформатора Y / Y0 – 12 (0) или Y/Δ – 11 (звезда – звезда с нейтральным проводом, группа 12; звезда – треугольник, группа 11); Uк % - напряжение короткого замыкания в % от номинального напряжения; I1Х % - ток холостого хода в % от номинального.
где U1н, U2н – номинальные линейные напряжения; I1н, I2н – номинальные линейные токи; мощность потерь холостого хода и короткого замыкания на три фазы Рх и Рк; номинальный КПД ηн, который задается при активной нагрузке (сos φ2 = 1) и при коэффициентах загрузки β=1 и β=0,5; группы соединений обмоток трансформатора Y / Y0 – 12 (0) или Y/Δ – 11 (звезда – звезда с нейтральным проводом, группа 12; звезда – треугольник, группа 11); Uк % - напряжение короткого замыкания в % от номинального напряжения; I1Х % - ток холостого хода в % от номинального.
Литература. [1]§ 9.1-9.11; [3] § 11.1-11.10; [4] § 10.1 – 10.6; [6] § 10.1.
Пример: для трехфазного трансформатора мощностью Sн = 100 кВА, группой соединения обмоток которого Y/Y0 – 0, известно: номинальное напряжение на зажимах первичной обмотки трансформатора U1н = 6000 В, напряжение холостого хода на зажимах вторичной обмотки U2н = 400 В, напряжение короткого замыкания Uк = 5,5%, мощность короткого замыкания Рк = 2400Вт, мощность холостого хода Рх=600 Вт, ток холостого хода I1х =0,07 I1н.
Определить:
1) сопротивление обмоток трансформатора R1, X1, R2 и X2;
2) сопротивление ветвей холостого хода Z0, R0 и X0;
3) угол магнитных потерь δ.
Построить характеристики трансформатора:
1) внешнюю характеристику U2 = f1(β);
2) зависимость η = f1(β) КПД от нагрузки β;
Коэффициент мощности нагрузки принять соs φ2 = 0,75. Составить Т-образную схему замещения трансформатора.
Решение:
Определяем номинальный ток первичной обмотки:
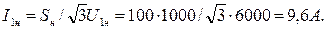
Определяем ток холостого хода и cos φ1х:
I1x = 0,07 I1н = 0,09 · 9,6 = 0,76 A
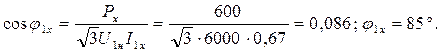
Находим угол магнитных потерь: δ = 90˚ - φ1х = 90˚ - 85˚ = 5˚.
Определяем сопротивления обмоток:
а) короткого замыкания
Zк = Uк.ф. / Iк.ф. = 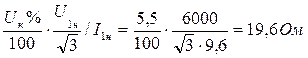 ;
;
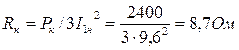 ;
;
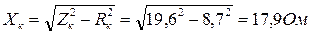 ;
;
б) первичной обмотки:
R1 = R2' = Rк/2 = 8,7/2 = 4,35 Ом;
Xd1 = X'd2 = Xк / 2 = 19,9 / 2 = 8,95 Ом;
в) вторичной обмотки:
R2 = R2'/n2 = 4,35/225 = 0,0193 Ом;
Xd2 = X'd2 / n2 = 8,95 / 225 = 0,0398 Ом;
где n = U1н/U2н = 6000 / 400 = 15.
Определяем сопротивления намагничивающей цепи (ветви холостого хода):
 ;
;
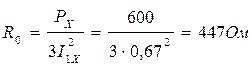 ;
;
 ;
;
Для построения внешней характеристики U2 = f1 (β) находим потерю напряжения во вторичной обмотке трансформатора:
ΔU2% = β (Uа cos φ2 + Uр Sin φ2) = β(2,4 · 0,75 + 4,95 · 0,66) = β · 5,074%, где Uа% = Uк cos φк = Uк % Rк /Zк = 5,5·8,7/19,9= =2,4%;
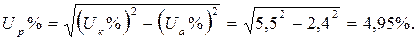
Напряжение на зажимах вторичной обмотки трансформатора определяем по формуле:
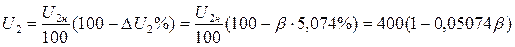 .
.
Задаваясь значением β = 0…1, находим U2 (табл. 2.1).
Таблица 2.1
| β | 0,01 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
| U, В | 399,8 | 397,97 | 395,94 | 393,92 | 391,89 | 398,86 | 387,83 | 385,80 | 383,78 | 381,75 | 379,72 |
| η | 0,555 | 0,924 | 0,956 | 0,965 | 0,967 | 0,969 | 0,967 | 0,966 | 0,964 | 0,963 | 0,962 |
Расчет КПД производим по формуле и данные сводим в табл. 2.1. полученные характеристики показаны на рис. 2.14.
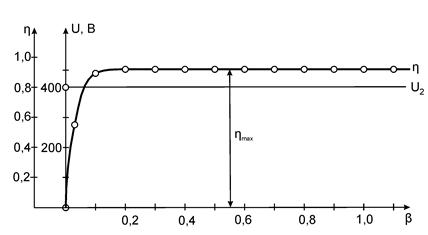
Рис. 2.14
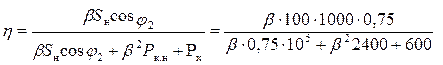
Определяем, при какой нагрузке трансформатор имеет максимальный КПД:
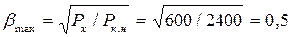
Составляем Т-образную схему замещения трансформатора (рис. 2.15).

Рис. 2.15
Вопросы для самопроверки.
1. Дайте полное определение коэффициента трансформации.
2. Какие параметры определяются из опытов холостого хода и короткого замыкания?
3. Напишите уравнения электрического состояния трансформатора.
4. Напишите уравнения МДС трансформатора.
5. Напишите общее выражение для КПД трансформатора.
6. Что называется приведенными величинами вторичной обмотки?
7. Какие потери энергии возникают в нагруженном трансформаторе?
8. Для какой цели применяются трансформаторы?
9. Какие факторы влияют на значение напряжения во вторичной обмотке?
Дата добавления: 2015-04-16; просмотров: 353; Мы поможем в написании вашей работы!; Нарушение авторских прав |