ТЕХНИКО-ЭКОНОМИЧЕСКОЕ ОБОСНОВАНИЕ НАДЕЖНОСТИ В ЭНЕРГЕТИКЕ

Надежность является важнейшим свойством электроснабжения в силу особенностей процесса производства и распределения энергии. Отсутствие возможностей создания запасов электроэнергии, быстротечность протекающих процессов, высокая зависимость народного хозяйства от своевременной подачи электроэнергии могут привести к значительному экономическому ущербу при нарушении надежности электроснабжения.

Для обеспечения надежности энергоснабжения используются такие методы, как повышение надежности элементов системы, недогрузка работающего оборудования, дублирование элементов, резервирование систем. Каждый из этих путей требует дополнительных затрат в систему электроснабжения и позволяет снизить ущерб, возникающий при нарушении, надежности электроснабжения. Соизмерение затрат и результатов дает ответ о целесообразных методах и уровне обеспечиваемой надежности.

(4.18)

где ∆З_R — повышение приведенных затрат в обеспечение надежности; ∆K_R, ∆И_R — повышение соответственно единовременных и ежегодных расходов, определяемых уровнем надежности R; 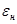— коэффициент эффективности дополнительных капиталовложений; ∆М (Y_R) — математическое ожидание снижения ущерба при надежности R.

При дублировании элементов или резервировании систем вероятность отказа технической системы вычисляют по формуле

(4.19)

где Q_i — вероятность отказа i-го элемента или системы.

При одинаковых элементах расчетная формула имеет вид

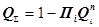
где n — число резервных элементов (систем), подключенных параллельно.

В системах с последовательно соединенными элементами ненадежность вычисляется по формуле

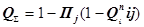(4.20)

где j — номер последовательно включенного элемента (системы).

Ущерб в системах электроснабжения может быть сложной функцией времени, глубины и характера повреждения, свойств потребителей электроэнергии. Упрощенный расчет ущерба выполняют по зависимости

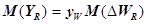(4.21)

где Y_W, — средняя величина ущерба по группе потребителей при недоотпуске 1 кВт • ч электроэнергии; 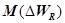— математическое ожидание недоотпуска электроэнергии при нарушении надежности электроснабжения.

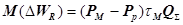(4.22)

где Р_м , Р_р - соответственно максимальная (расчетная) нагрузка потребителя и возможный резерв мощности из другого (резервного) источника энергии; т — число часов использования максимальной нагрузки.

Ненадежность отдельных элементов системы электроснабжения можно приближенно оценить по формулам:

линии электропередачи

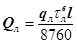(4.23)

где q_л — удельное число отказов 1 км линии; l - протяженность линии; — среднее время восстановления линии после отказа;

трансформаторы и выключатели:

,

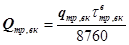где q_тр,вк — среднее число отказов трансформатора или выключателя; 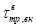— среднее время восстановления оборудования после отказа.

Капиталовложения, связанные с дублированием или резервированием, определяют по такой зависимости:

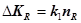
где k₁ — капиталовложения в один элемент (систему); n_R — число дублирующих (резервирующих) элементов или систем. Показатель k₁ можно рассчитать по формулам, приведенным в гл. 2, для оценки стоимости основных фондов элементов энергетики.

Ежегодные затраты, обусловленные обеспечением определенного уровня надежности путем резервирования или дублирования, можно рассчитать по формуле

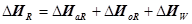
где ∆И_aR — амортизационные отчисления по системе с учетом резервных элементов; ∆И_oR — ежегодные затраты на ремонт и обслуживание системы; ∆И_W — стоимость потерь электроэнергии в системе электроснабжения.

∆И_W=з_W∆W_R,

где З_W — удельные замыкающие затраты на компенсацию потерь электроэнергии; ∆W_R — потери электроэнергии в системе электроснабжения с учетом резервных элементов.

Потери электроэнергии в различном оборудовании системы электроснабжения можно рассчитать, по следующим зависимостям:

линия электропередачи:

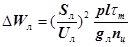(4.25)

где S_л — полная передаваемая по ЛЭП мощность; U_л — фазное напряжение линии; р — удельное сопротивление проводникового материала; q_л — сечение линии; l — длина линии электропередачи; n_ц — число цепей линии электропередачи;

трансформаторы:

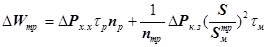(4.26)

где ∆Р_х.х , ∆Р_к.з — потери холостого хода и короткого замыкания трансформаторов, кВт; 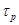, — время работы и максимальных потерь, ч/год; n_тр — количество' трансформаторов; S, — соответственно нагрузка элемента и номинальная мощность трансформатора, кВ • А.

В некоторых случаях возникает проблема оптимизации надежности систем в условиях ограничений, например по стоимости, весу, занимаемой площади и др. Решить задачу можно на основе использования либо методов оптимального планирования, либо упрощенного подхода с использованием неопределенных множителей Лагранжа.

Пусть имеется система из подсистем, в каждой из которых можно осуществить дублирование введением 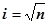элементов.

Надежность такой системы определяется как вероятность безотказной работы и рассчитывается как

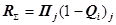
Необходимо найти такую структуру системы, для которой достигается максимальная надежность и выполняются ограничения по стоимости и весу:

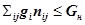
(4.28)

где k_i — стоимость одного элемента i-го типа; n_ij. — число i-х элементов в j-й подсистеме; g_i - вес одного элемента i-го типа; G_н - предельное (граничное) значение веса системы; К_н — предельные капиталовложения в систему.

Пусть имеется система, состоящая из j подсистем (распределительное устройство подстанции, система питания собственных нужд электростанции, защита генератора и т.п.), в каждой из которых может быть n_ij. параллельно включенных элементов i-го типа. Примем также, что подсистема работоспособна, если исправен хотя бы один из ее элементов. Предположим также, что должны быть выполнены r ограничивающих условий вида

где а_ri — удельный расход фактора r на i-й элемент, например капиталовложения, вес, объем и др.

В соответствии с (4.27) надежность системы можно вычислить по формуле

где Q_i — вероятность отказа элемента i; n_ij — число элементов i в подсистеме j.

Задача оптимизации надежности такой системы состоит в нахождении вектора R(n), компонентами которого являются положительные целые числа, обеспечивающего максимизацию функции R_∑ при выполнении условий (4.28).

Решение задачи может быть основано на построении доминирующей последовательности, состоящей из доминирующих векторов. Доминирующим называется вектор, обеспечивающий в экономических задачах для одного и того же уровня надежности меньшую стоимость системы. Построение доминирующей последовательности ведут следующим образом. Сначала строят доминирующую последовательность для подсистем 1 и 2. К полученному вектору добавляют подсистему 3 и строят доминирующую последовательность для совокупности подсиcтем 1, 2 и 3. Процесс продолжается до тех пор, пока не будут рассмотрены все подсистемы, т. е. пока не будет построена доминирующая последовательность для всей системы в целом. Решением задачи является вектор, выбираемый из доминирующей последовательности и характеризующийся наибольшей надежностью. По этому вектору находят соответствующий состав системы путем анализа доми-нирующих последовательностей в обратном направлении.

При практическом использовании описанного метода построения доминирующей последовательности целесообразно сделать следующие допущения, позволяющие существенно сократить процесс расчетов.

1. Вместо выражения (4.27) для определения надежности системы, состоящей из двух подсистем, пользуются формулой

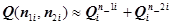
где Q(n_1i,n_2i) - вероятность отказа системы, имеющей соответственно в подсистемах 1 и 2n_1i и n_1i параллельно включенных элементов; 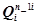- вероятность отказа подсистемы 1, имеющей n_1i элементов;

- вероятность отказа подсистемы 2 с элементами.

Аналогично для системы, состоящей из т подсистем, можно приближенно записать

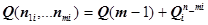
где Q(m - 1) — вероятность отказа совокупности подсистем, включающей т- 1 подсистем; 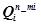- вероятность отказа подсистемы m, (1, .... m - 1) — номера подсистем, входящие в группу, имеющую вероятность отказа Q (m - 1).

Погрешность, получаемая при использовании такого допущения в оценке надежности системы R_Σ, не превосходит (1 - )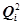

2.При сравнении пары векторов в процессе нахождения доминирующей последовательности полезно рассмотреть допустимые погрешности по затратам, а также по ненадежности. В этом случае, если какие-либо два вектора отличаются по затратам на величину δ₃ или менее, они считаются идентичными. То же самое можно сказать о векторах, отличающихся друг от друга по ненадежности на величину δ_Q.

3. Целесообразно использовать наибольшие начальные значения , при которых затраты на систему будут не больше заданных при условии, что резервирование осуществляется только элементами каждoй из подсистем в отдельности.

Метод нахождения таких наибольших начальных значений заключается в следующем:

а) прибавляют по одному элементу каждого типа до тех пор, пока, наконец, при добавлении очередного элемента не нарушится хотя бы одно из ограничений;

б) вычисляют значение надежности R_ij для построенной таким образом системы;

в) из выражения R_ij ≤ 1 - определяют — минимальное количество элементов i-го типа, необходимых для достижения надежности равной R_ij и более.