ПРОГНОЗИРОВАНИЕ РАЗВИТИЯ ЭНЕРГЕТИКИ

Под прогнозированием понимают научно обоснованное предвидение социально-экономических процессов и научно-технических тенденций развития экономики, базирующееся на изучении объективных экономических законов, моделировании и анализе будущего развития с целью формирования и оптимизации планов. Необходимость прогнозирования связана с инерционностью развития производственных и экономических систем, с большими затратами на разработку новой техники и технологии, сравнительно длительными сроками их освоения и относительно быстрым старением техники и технологии.

Основными принципами разработки прогнозов являются :

системность прогнозирования, т. е. взаимоувязка и соподчиненность прогнозов объекта прог-нозирования и его элементов и прогнозного фона;

вариантность прогноза;

непрерывность прогнозирования, требующая постоянной корректировки прогноза по мере накопления информации;

верифицируемость прогнозов, требующая достоверности, точности и обоснованности прогнозов;

рентабельность прогнозирования, т. е. получение экономического эффекта от использования прогноза с учетом затрат на его разработку.

Всю совокупность методов прогнозирования можно разделить на три основных класса:

статистические (экстраполяция тенденций), базирующиеся на распространении выводов, сделанных в результате изучения состояния объекта прогнозирования в прошлом и настоящем, на его состояние в будущем;

экспертных оценок, основанных на статистической обработке мнений специалистов-экспертов об объекте прогнозирования;

моделирования, заключающегося в построении модели изучаемого объекта с целью анализа его поведения в будущем.

Статистические методы прогнозирования наиболее распространены и основываются на построении и анализе динамических рядов, характеризующих поведение системы или объекта прогнозирования в прошлом и настоящем, и экстраполяции полученных тенденций на прогнозируемый период.

Экстраполяция базируется на ряде допущений: развитие явления может быть с достаточным основанием охарактеризовано плавной траекторией-трендом; основные условия, определяющие тенденцию развития в прошлом, не претерпевают существенных изменений в будущем.

В экономическом анализе оценки тенденций развития и прогнозирование могут выполняться с помощью таких простейших показателей, как средний темп роста, скользящие и взвешенные средние, экспоненциальные средние. Так, если тенденция развития у в исследуемом временном интервале характеризуется постоянным темпом роста с приращениями:

абсолютным средним арифметическим

и относительным

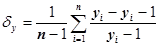
где y(y₁, ..., у_i, ..., y_n) - значения параметров динамического ряда объемом n, то прогнозное значение у на любой год, t = 1, 2, ...,T, будет равно

;

Корреляционный анализ может быть использован либо для описания с помощью аналитической функции изменения прогнозируемого показателя y во времени t (анализ временных рядов), либо для установления многофакторной связи между прогнозируемым y и рядом других показателей ( х, z, ...). В отличие от анализа временных рядов установление множественной корреляции позволяет учесть динамику систем, выделить важнейшие факторы, которые определяют их состояние, и т.д.

Исходной информацией для прогноза служат статистические данные. Статистические зависимости при этом аппроксимируются известными аналитическими функциями - уравнениями регрессии. Характер уравнения регрессии определяется на основе общих представлений о виде связи или путем прямого перебора известных функций:

линейной функции

у=а +bt; (4.29)

параболы второй степени

y =а + bt+ сt²; (4.30)

простой экспоненциальной (показательной) функции

y=ab^t, (4.31)

модифицированной экспоненциальной функции

у=а - вс^-t (4.32)

степенной функции

y=аt^b (4.33)

где a, b и с — коэффициенты уравнений регрессии.

Уравнение множественной корреляции в предположении о линейном характере взаимосвязи переменных у, х, z имеет вид

у =а + bx + cz . (4.34)

Коэффициенты а, в и с в (4.29.- 4.34) могут быть получены с использованием метода наименьших квадратов

(4.35)

где y_рi,, y_фi, — расчетное и фактическое значение анализируемого показателя.