ОБЩАЯ ХАРАКТЕРИСТИКА ЗАДАЧ И МЕТОДОВ РЕШЕНИЯ ПРИ НЕОПРЕДЕЛЕННОСТИ

Понятие риска в процессе общественного развития известно с древних времен. В общем случае риск обусловлен вероятностным проявлением тех или иных исходов (состояний) при выбранных способах действий. В тех случаях, когда нельзя получить вероятностные оценки исходов, решения приходится принимать в условиях полной неопределенности. Учет риска и неопределенности в задачах экономического анализа требует специальных методических подходов .

Неопределенность проявляется как результат взаимодействия множества факторов, основными из которых являются: невозможность точного описания условий развития больших систем; множественность и противоречивость конечных целей; неоднозначность и погрешность исходной информации.

Рассматривая современную теорию принятия решений, можно выделить три характерные ситуации выбора решения.

Первая ситуация возникает при условии, когда выбор решения осуществляется при полной определенности, т. е. каждому возможному действию соответствует вполне однозначный исход. При сравнительном анализе вариантов для этой ситуации используется критерий минимума приведенных затрат при тождестве народнохозяйственного эффекта.

В реальных условиях возникают ситуации, когда каждому действию может соответствовать множество исходов. Если этим исходам можно приписать определенные вероятности их появления, то имеем случай выбора решений в условиях неопределенности в форме риска.

Поскольку на формирование затрат воздействует множество случайных факторов, они также являются случайной переменной. Случайные величины могут быть двух типов:

дискретными, когда случайная величина может принимать конечное число значений с соответствующими вероятностями;

непрерывными, если случайная величина может принимать все значения на определенном интервале.

Таким образом, при анализе случайных величин центральной проблемой является получение функции распределения вероятностей. Решение ее зависит от методов исследования и наличия статистической информации. Пусть х — случайная переменная с функцией распределений F(х). При непрерывной и дифференцируемой F(х) имеем

f(х) = F'(х) ,

где f(х) — плотность случайной величины.

Поэтому, если ввести обозначение вероятности через р, то в расчетах необходимо использовать следующие соотношения:

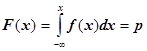
Очевидно эти соотношения при замене знака интеграла на знак суммы должны применяться и для дискретных случайных величин.

Для последующего анализа задач в условиях неопределенности необходимо использовать показатели математического ожидания. Математическим ожиданием случайной переменной называется ряд

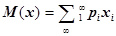(для дискретных случайных величин) ;

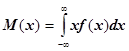(для непрерывных случайных величин) .

При изучении функций распределения вероятностей и показателей математического ожидания основными являются средние величины и центральные моменты 2-го порядка (дисперсии), которые определяются следующим образом:

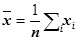
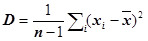
Показатель дисперсии является мерой вариации показателя от среднего значения, поэтому его также используют в качестве меры риска . Этой мерой могут также служить показатели среднеквадратичного отклонения и коэффициент вариации .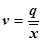

В последующих задачах выбора решений на множестве вариантов необходимо использовать критерии:

М(З_і)=min_i(M(З₁),…,М(З_n)) (6.1)

D(З_і)=min_i(D(З₁),…,D(З_n)) (6.2)

Выбор решения в случае с полной неопределенностью характеризуется тем, что каждому действию соответствует множество исходов, но вероятности их появления не могут быть заданы: Для задач этого типа необходимо иметь конечное множество действий (вариантов) и конечное множество состояний (исходов). По этим исходам должна быть построена платежная матрица, в которой строки определяют способы действия (стратегии), а столбцы — возможные исходы. На пересечении строк и столбцов проставляются элементы, которые показывают достижение конечных результатов. При экономическом анализе эти результаты могут быть описаны затратами, эффектами, отношениями эффекта к затратам и т.д. Таким образом, экономическое обоснование решений в условиях неопределенности должно начинаться с построения платежной матрицы

З=(З_ij)

где i = 1…n — стратегии действия,j = 1…m,— возможные исходы.

Для выбора решений на основе платежной матрицы современная практика может применять ряд критериев.

1. Критерий недостаточного основания, который исходит из принципа равновероятности возможных исходов. Для его реализации необходимо по каждой стратегии найти величину средних затрат, а затем выбирается решение по условию

(6.3)

2. Критерий минимакса затрат, основанный на следующем принципе: для каждой стратегии из возможных исходов выбирается такое состояние, которое приводит к наибольшим затратам. После такого сжатия матрицы в один столбец определяется элемент с наименьшими затратами, т. е. наилучшая стратегия определяется по условию

min_imax_j(З_ij) (6.4)

3. Критерий минимакса потерь, исходящий из преобразования платежной матрицы затрат в матрицу потерь. Эта операция осуществляется следующим образом:

1) в каждом столбце исходной матрицы находят элемент с наименьшими затратами;

2) для других элементов каждого столбца определяют потери в виде разности фактических и наименьших затрат;

3) на основе построенной матрицы потерь выбирают стратегию по условию

min_imax_j(∆З_ij) (6.5)

В реальных задачах обоснования решений возможны случаи, когда рассмотренные выше три критерия выбора приводят к различным стратегиям, а значит, вновь возникает ситуация неопределенности. Для ее преодоления можно воспользоваться следующим способом.

а основе матрицы, в которой столбцы состоят из векторов, по соответствующим критериям строим новую матрицу, состоящую из элементов в виде отношения абсолютных оценок каждого столбца

к минимальной оценке этого столбца. В результате этого получаем индексную матрицу

е = (е_ik) (6.6)

где k = 1…r обозначает соответствующий критерий выбора. Из полученной таким образом матрицы находим оптимальную чистую стратегию по условию

(6.7)

В тех случаях, когда допустимой является комбинация чистых стратегий, задачу можно решить в смешанных стратегиях, используя для этой цели математический аппарат теории игр.

При решении экономических задач приходится иметь дело с собственно неопределенными показателями . К ним относятся такие показатели, которые могут принимать различные значения в зависимости от неизвестного исхода тех или иных событий или действий. Характерным примером таких показателей являются уровни электропотребления на перспективу, поскольку их значения определяются еще не принятыми решениями относительно темпов развития народного хозяйства. Наиболее сильное влияние на выбор технических решений оказывают вариации экономических показателей, которые вызываются различными внешними условиями. Изменение экономических показателей может быть связано с природно-климатическими факторами, темпами развития научно-технического прогресса и т.д. В расчетах указанные показатели должны задаваться в виде нескольких альтернативных значений. Набор этих значений образует множество исходных условий, которые в конечном счете .определяют возможности реализации тех или других решений.

Нахождение представительного набора сочетаний этих показателей требует применения специальных методов и алгоритмов. При решении ряда других задач можно ограничиться варьированием значений двух-трех исходных показателей, что не создает больших трудностей для составления представительных сочетаний.

Рассмотрим Структурную задачу, в которой будут варьироваться удельные приведенные затраты на двух уровнях . При формировании структуры прироста мощностей энергосистем на базе т энергетических объектов число возможных комбинаций целевой функции будет равно 2m. Пронумеровав эти комбинации (состояния) в последовательности s = 1…k, получим k задач следующего вида:

Min f_s(x₁,…,x_m) (6.8)

∑_ix_i=∆N *

где ∆N — необходимый прирост мощности энергосистемы за определенный плановый период времени ( год, пять лет и т.д.).

Для генерации стратегий развития системы при фиксированных состояниях s можно воспользоваться аналитической моделью, которая легко преобразуется в функцию Лагранжа:

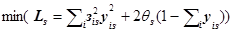(6.9)

Беря от (6.9) частные производные по y_is = и 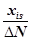и приравниваяих к нулю, получим

(6.10)

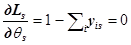
Из условия (6.10) находят численную оценку множителя

(6.11)

и удельные веса энергетических объектов y_is. Полученные решения определяют стратегии развития энергосистемы, которым можно приписать следующую нумерацию:

r = s =1…k .

При r =s будут иметь место вариации затрат, поэтому их надо свести в платежную матрицу "стратегии—состояния", на основе которой выбирается оптимальная стратегия.