
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ЭКОНОМИЧЕСКОЕ ОБОСНОВАНИЕ КОЭФФИЦИЕНТА РИСКА И НАГРУЗОЧНОГО РЕЗЕРВА В ЭНЕРГОСИСТЕМАХ
Достижение основных целей функционирования энергосистем, обеспечивающих экономичное и надежное энергоснабжение потребителей, осуществляется путем резервирования мощности и создания запасов первичных энергоресурсов. Расчетные электрические нагрузки, в том числе и максимальная, носят вероятностный характер, что необходимо учитывать при проектировании и планировании энергобалансов. Одной из задач формирования баланса мощности является определение величины нагрузочного резерва, который обеспечивает компенсацию колебаний и непредвиденного повышения нагрузки ∆Р сверх учтенной величины максимума Рm .
Поскольку ∆Р является случайной величиной, установление величины резерва R должно основываться на задании вероятности того, что колебания нагрузки не превысят резервной мощности. Эту вероятность можно назвать уровнем (коэффициентом) надежности и обозначить через р. Вместо этого показателя можно использовать вероятность противоположного события, которую называют коэффициентом риска и обозначают через q. Этот коэффициент характеризует вероятность того, что резерв в системе окажется недостаточным для компенсации возросшей нагрузки ∆Р.
При известной функции распределения F(∆Р) и заданном коэффициенте надежности р величина нагрузочного резерва R = ∆Р легко определяемся из условия
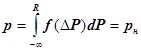 (6.12)
(6.12)
или
 (6.13)
(6.13)
qн=1-pн
Решение сформулированной задачи (6.12), (6.13) по определению резерва R рекомендуется провести самостоятельно, используя для этого нормальное распределение случайной переменной или распределение Пуассона.
Задача определения резерва R является экономической, поскольку при R > ∆Р появляются дополнительные затраты по созданию и содержанию резервной мощности.
ЗR = зR(R-∆Р) (6.14)
где зR — удельные приведенные затраты в единицу резервной мощности. При R < ∆Р в системе появляется дефицит производственных возможностей, который обусловливает экономические потери (ущерб) в размере
Зу=зу(∆Р-R) (6.15)
где зy — удельный ущерб от дефицита мощности.
Поскольку ∆Р является случайной переменной, для обоснования величины R необходимо минимизировать математическое ожидание суммарных затрат:

х f(∆Р)d∆Р-→min (6.16)
Математическое ожидание затрат M(3∑) состоит из двух слагаемых:
первое соответствует случаю R > ∆Р;
второе — R < ∆Р.
Задача заключается в нахождении величины Н такой, чтобы М(3∑) достигало минимума. Для ее решения необходимо взять производную по R и приравнять к нулю, используя теорему математического анализа о дифференцировании под знаком интеграла. Производные по R от интегралов будут определяться выражениями:
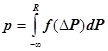 ;
; 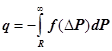
С учетом полученных соотношений условие оптимальности для определения q можно получить из выражения
dМ(3∑) =(зRр- зуq)dR= 0; (6.17)
зR(1-q)-зyq=0. (6.18)
Из (6.18) получим оптимальное значение коэффициента риска
opt q= 
и соответственно уровня надежности
opt p= 
Воспользовавшись функцией F(х), которая для рассматриваемой задачи может быть записана в виде р(R), при заданном орt р находят оптимальную величину резерва. Это можно сделать либо графическим способом, либо в табличной форме с использованием методов интерполяции.
При небольших дополнениях рассмотренный методический подход можно применить к решению и других задач проектирования и планирования энергетики.
Постановка и решение задач по рассмотренной выше методике прежде всего должна быть основана на статистической информации относительно частот колебаний ∆Р. В тех случаях, когда этой информации нет, но есть предположения относительно закона распределения вероятностей, то решения должны базироваться на этих законах. При задании, например, нормального распределения, что подтверждается практикой анализа нерегулярных колебаний нагрузки, для построения интегральной функции распределения вероятностей достаточно иметь оценки среднего значения ∆Р и дисперсии ∆р. Если затруднительно задать и эти параметры, то задача должна решаться в условиях полной неопределенности.
Вторая группа исходных данных включает экономические показатели затрат на создание и содержание резерва и ущерба от его недостаточности. Опыт эксплуатации и проектирования энергосистем позволил получить такие оценки, которые и должны быть использованы в технико-экономических обоснованиях. При этом, конечно, необходимо учитывать, что удельные затраты зR и зy могут иметь значительные вариации, которые будут обусловливать изменения уровня надежности и, следовательно, резерва энергосистемы. Отсюда важной задачей является установление пределов этих изменений, которые будут характеризовать зону неопределенности полученного решения.
Для практического использования рассмотренных методических положений сформулируем основную задачу с некоторыми дополнениями технико-экономического анализа.
Дата добавления: 2015-04-16; просмотров: 256; Мы поможем в написании вашей работы!; Нарушение авторских прав |