
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ОПТИМИЗАЦИЯ НАДЕЖНОСТИ ЭНЕРГОСНАБЖЕНИЯ
Надежность работы агрегата энергоблока характеризуется в первом приближении коэффициентом готовности:
 (7.1)
(7.1)
где  , — время нахождения агрегата в рабочем состоянии, включая время резерва;
, — время нахождения агрегата в рабочем состоянии, включая время резерва;  — продолжительность аварийного состояния агрегата. Аварийность агрегата характеризуется показателем
— продолжительность аварийного состояния агрегата. Аварийность агрегата характеризуется показателем
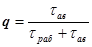 (7.2)
(7.2)
Для системы, состоящей из m однотипных агрегатов с единичной мощностью N, вероятности всех возможных состояний системы могут быть найдены из разложения бинома Ньютона
 (7.3)
(7.3)
где  = рjm. — вероятность одновременного выхода из строя агрегатов.
= рjm. — вероятность одновременного выхода из строя агрегатов.
Число сочетаний из m элементов по j
 (7.4)
(7.4)
Первый член этого разложения показывает вероятность рабочего состояния всех агрегатов рom, а последний — вероятность аварийного состояния всех агрегатов, т. е.
рmn ; ∑jpjm =1.
Выход из строя одного агрегата приводит к снижению мощности системы на N, а j агрегатов — на jN. Поэтому надежность энергоснабжения может быть оценена как вероятность отсутствия дефицита мощности в системе.
Обозначим через р-jm вероятность снижения мощности системы на мощность агрегатов, т. е. jN, тогда ряд распределения вероятностей всех возможных состояний системы перепишется так:
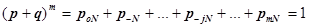 (7.5)
(7.5)

Таким образом, при отсутствии резервных агрегатов в системе надежность энергоснабжения р будет равна вероятности работоспособного состояния всех агрегатов: ро =poN = pm. Это можно записать так же, как, если количество резервных агрегатов в системе r=0.
При установке в системе одного резервного агрегата надежность энергоснабжения возрастет до величины
р0 = р 0N+р_N
и т.д
при r резервных агрегатов -
 (7.6)
(7.6)
Отсюда, если задать нормативное значение надежности энергоснабжения ро, то можно определить необходимое количество резервных агрегатов, а следовательно, и мощность аварийного резерва.
Это количество резервных агрегатов может быть найдено подбором, исходя из условия
 (7.7)
(7.7)
или
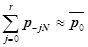 (7.8)
(7.8)
В практике проектной работы величина р0 задается на уровне 0.999. Однако возможен и экономический подход к оценке надежности энергоснабжения, а следовательно, и величины аварийного резерва (числа резервных агрегатов и их мощности). Этот подход основываемся на сопоставлении вероятного ущерба в народном хозяйстве от недоотпуска электроэнергии в связи с аварийным выходом энергоагрегатов из строя, с затратами на создание резерва мощности в ЭЭС.
В соответствии с изложенным • ранее математическое ожидание дефицита энергии в результате вероятных аварий при отсутствии резерва может быть найдено из выражения
 (7.9)
(7.9)
где j=1…m — количество вышедших из строя агрегатов.

Установка резервных агрегатов будет уменьшать вероятность ограничения мощности в системе и, следовательно, уменьшать математическое ожидание дефицита мощности и энергии. При установке одного резервного агрегата мощностью N дефицит появится лишь при выходе из строя двух агрегатов, при установке двух резервных агрегатов дефицит возникает лишь в случае выхода из строя трех агрегатов и т.д.
Поэтому при установке г резервных агрегатов величину дефицита энергии можно определить по формуле (принятые обозначения приведены в табл. 8.1)
 (7.10)
(7.10)
Для определения оптимального числа резервных агрегатов r сравнивают постоянную составляющую приведенных затрат на резерв ЗR с математическим ожиданием ущерба от недоотпуска энергии yR
YR=yr∆wr (7.11)
ЗR=зRNr=(єн+а∑)kNNr (7.12)
где уR - удельный ущерб у потребителя [Грн/ (кВт • ч) ] от недоотпуска ему энергии; ЗR - удельные приведенные затраты в резерв, Грн/кВт; єн - нормативный коэффициент экономической эффективности дополнительных капиталовложений; а∑ — доля постоянной части эксплуатационных расходов от капиталовложений в электростанцию; kN — удельные капиталовложения на единицу установленной мощности резервных электростанций, Грн/кВт.
Расчет производится путем сравнения различных вариантов числа установленных резервных агрегатов. Такой расчет удобно производить в табличной форме ( см. табл.7.1).
Таблица 7.1.
Определение оптимальной величины аварийного резерва
| Количество резервных агрегатов r | Мощность резерва NR | Дефицит энергии при числе резервных агрегатов ∆Wr | Затраты на резерв 3R | Ущерб yR | ЗR+yR |
| W0 | yR∆W0 | yr∆w0 | |||
| N | ∆W1 | ЗRN | yR∆W1 | ЗRN+yR∆W1 | |
| : . r | : . rN | : . ∆Wr | : . зRrN | : . yr∆wr | : . зRrN+yR∆Wr |
Оптимуму соответствует минимальное значение зR + YR или условие ∆ЗR > ∆yR, т. е. прирост затрат на резерв больше или равен уменьшению ущерба.
Для найденного значения — ropt находим  = roptN и надежность энергоснабжения
= roptN и надежность энергоснабжения
 (7.13)
(7.13)
Коэффициенты третьей строки треугольника Паскаля 1, 3, 3, 1 совпадают с коэффициентами разложения бинома третьей степени:
(р+q)3=1pз+3о2q+3рq2+1q3 . (7.14)
Элементы 1,6, 15, 20, 15, 6, 1 совпадают с элементами разложения бинома шестой степени
(р + q)6 = 1р6 + 6р5q + 15р4q3 + 20р3q3 + 15р2q4 + 6рq5 + 1 q6 .
Дата добавления: 2015-04-16; просмотров: 276; Мы поможем в написании вашей работы!; Нарушение авторских прав |