ПРОБЛЕМА ТОЧНОСТИ В ЗАДАЧАХ ТЕХНИКО-ЭКОНОМИЧЕСКИХ ОБОСНОВАНИЙ

Результаты технико-экономического анализа и выбор оптимального решения, особенно на стадиях долгосрочного планирования и прогнозирования, в значительной степени определяются объективными условиями задания исходной информации, той или иной степенью ее точности.

Понятие "точность" связано с погрешностью измерений. Погрешность измерения представляет собой отклонение результата измерения от истинного значения измеряемой величины.

Если погрешность измерения выражена в единицах измеряемой величины, то она называется абсолютной и может быть определена как

∆x = х -x₀ ,

где х — значение, полученное при измерении; x₀ — истинное значение измеряемой величины.

Однако, поскольку истинное значение измеряемой величины остается неизвестным, на практике можно найти лишь приближенную оценку погрешности измерения.

Отношение абсолютной погрешности измерения к истинному значению измеряемой величины (а на практике обычно к измеренному ее значению ) называют относительной погрешностью измерения.

Точность измерения количественно выражают обратной величиной модуля относительной погрешности

.

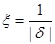Поэтому в дальнейшем изложении в качестве показателя точности будет в основном использоваться относительная погрешность измерения.

Методы "теории ошибок" могут быть применены и к анализу решений задачи линейного программирования. В этом случае можно использовать следующие подходы.

Погрешность в задании исходных данных и в определении основных результатов решения задачи характеризуется:

а) величиной абсолютной ошибки (погрешности) показателя Ф:

∆Ф=Ф - Ф_р, (7.24)

где Ф, Ф_p — абсолютное значение анализируемого показателя (коэффициента матрицы условий а, коэффициента целевой функции с, значения функционала L(х) и т.д.) соответственно фактическое и в оптимальном плане.

б) величиной относительной ошибки (погрешности) показателя Ф:

(7.25)

Пусть известен оптимальный вектор прямой задачи х( , ..., ), где

m — число переменных в оптимальном базисе. Тогда для оптимального решения можно записать

(7.26)

(7.27)

Для анализа погрешности решения этой задачи могут быть использованы методы оценки ошибки косвенных измерений, разработанные а классической теории ошибок .

Таким обрезом, если известны ошибки в задании коэффициентов матрицы условий (A) — ∆а_ij, коэффициентов ограничений ∆b_i и коэффициентов функционала ∆с_j, то связь между абсолютными ошибками в задании этих коэффициентов и ошибками в расчете значений переменных ∆х_j. может быть выражена следующими формулами:

а) для ограничений

(7.28)

б) для функционала

(7.29)

Из анализа формул (7.28), (7.29) следует, что главная сложность в их использовании состоит в нахождении ошибок расчета переменных х_j, так как они определяются в результате решения задачи.

Возможны следующие методы оценки погрешности решения задачи линейного программирования.

1. Метод, основанный на непосредственном определении абсолютных ошибок в расчете переменных ∆x_j. Поскольку ошибки в задании коэффициентов матрицы условий ∆а_ij и коэффициентов ограничений ∆b_i могут полагаться известными (задаваемыми на основе анализа прошлого опыта), возможно решение системы (8.28) относительно ∆x_j. Эта система из т переменных ∆х_j и m уравнений может быть решена либо методом Крамера, либо методом исключения Гаусса:

(7.31)

где D_мо — определитель главной матрицы; D_∆xj — определитель матрицы, полученной путем замены столбца переменной ∆х_j, столбцом свободных членов.

Найденные значения ошибок переменных ∆х_j. совместно с ошибками в задании коэффициентов функционала ∆с_j. подставляются в формулу (7.29), что и дает искомую ошибку в расчете функционала ∆L( 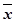). В реальных условиях эта система часто может быть несовместной, в результате чего получить решение невозможно.

2. Метод, основанный на предположении о равном влиянии ошибок в расчете переменных на ошибку функции. Исходным пунктом этого метода является то, что поскольку конкретные значения ошибок не известны, то можно предположить, что они оказывают одинаковое влияние на погрешность в расчете значения функции. Тогда по каждому ограничению i можно записать

,

из чего следует, что ошибка в расчете переменной по ограничению равна

(7.32)

где m — число переменных; а_ij — коэффициент при переменной х_ij в ограничении i.

Так как каждая переменная может быть определена из различных ограничений, то за ее расчетное значение принимается минимальное среди найденных из каждого ограничения, т. е.

Далее, как и в предыдущем случае, подставляем найденные значения ∆х_j в формулу для определения ошибки функционала. Изложенный подход проще предыдущего, но дает некоторое искажение результата из-за принятых допущений.