Для линейных уравнений

;

.

На основе известных преобразований, связанных с отысканием экстремума функции нескольких переменных, т. е., дифференцируя функцию F по искомым переменным а, b и с и приравнивая производную к нулю, получают систему линейных уравнений, позволяющую найти неизвестные а, Ь и с.

Выбор формы кривой является одной из важнейших проблем при выравнивании динамических рядов. Существуют различные подходы, которые позволяют выбрать форму кривой, адекватную действительной динамике. Наиболее простой — визуальный, на основе графического изображения динамического ряда, дополненный анализом процесса развития по существу. Второй подход заключается в подборе такой функции из числа возможных, которая наилучшим образом описывает динамический ряд. Критерием для отбора функции могут служить следующие показатели:

среднеквадратичное отклонение

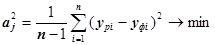(4.36)

корреляционное отношение

(4.37)

коэффициент вариации n

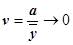
(4.38)

Большим преимуществом математических методов прогнозирования является обогащение прогнозов путем определения доверительных интервалов и доверительных границ для прогнозируемых показателей. Доверительный интервал для прогноза характеризуется выражением

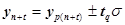(4.39)

где t_q - коэффициент, определяемый принятым уровнем доверия (q (0,1) ), зависящим от распределения случайной величины и объема выборки.

Для широко используемого нормального распределения могут быть приняты следующие значения коэффициента t_q:.

t_q = 1 при q = 0,84; t_q= 2 при q =0,97 и t_q = 3 при q= 0,997.

Доверительные границы прогнозируемого параметра (y_(n+t)min' y_(n+t)max) определяются

y_p(n+t) -t_qσ = y_(n+t)min ≤y_n+t,≤y_(n+t)max = y_p(tn+t) + t_qσ

Доверительные границы показывают, с какой вероятностью искомая прогнозируемая величина может попасть в интервал (y_min, y_max) Знание доверительных интервалов расширяет возможности прогнозирования, показывая, например, возможные резервы или дополнительные зоны поиска.

СПЕЦАЛЬНЫЕ РАЗДЕЛЫ КУРСА