Оценка качества импульсных систем

Общие соображения по оценке качества систем автоматического управления, рассмотренные в разделе 8, относятся и к импульсным системам.

Для оценки точности можно использовать величину ошибки в типовых режимах.

В режиме установившегося состояния при постоянном значении задающего воздействия и в режиме движения системы с постоянной скоростью при задающем воздействии, изменяющемся по закону где при отсутствии возмущения значение установившейся ошибки в дискретные моменты времени в соответствии с теоремой о конечном значении (11.17) определяется по формуле

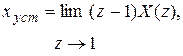(12.13)

где X (z) определяется выражением (11.24).

Следует отметить, что необходимость в использовании формулы (12.13) возникает только тогда, когда скважность импульсов на выходе формирующего устройства системы (рис.11.1, сигнал х^*). Если то в установившемся состоянии сигнал на выходе этого устройства 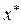будет постоянным и импульсная система может рассматриваться как непрерывная. В этом случае для оценки точности можно воспользоваться формулами, приведенными в разделе 8.3. Рассмотрим пример, подтверждающий сказанное выше.

Пример. Определить установившуюся ошибку импульсной системы (рис. 12.3) при задающем воздействии 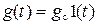, имеющей передаточную функцию разомкнутой системы (см. пример, раздел 11.2).

Решение. Найдем вначале установившуюся ошибку по формуле (12.13). В соответствии с (11.24), (11.7) изображение ошибки получим в виде:

(12.14)

Установившаяся ошибка

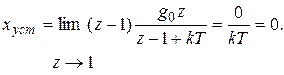(12.15)

Так как в данном примере формирующее устройство ФУ есть экстраполятор нулевого порядка, применим для определения формулу (8.6), выведенную для непрерывных систем.

Передаточная функция разомкнутой системы равна в этом случае передаточной функции непрерывной части:

(12.16)

Изображение ошибки по Лапласу

(12.17)

Установившаяся ошибка

(12.18)

Как видим, результаты (12.15) и (12.18) совпадают.

В режиме движения по гармоническому закону, когда 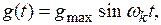частота обычно сравнительно мала, причем всегда При этом условии псевдочастота 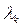в соответствии с (12.7) практически совпадает с реальной частотой и для расчетов можно использовать формулы (8.10) и (8.11), положив в них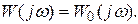

Специфической особенностью импульсных систем является возможность существования в них переходных процессов конечной длительности, полностью заканчивающихся за конечный промежуток времени. Для этого параметры системы должны быть выбраны так, чтобы корни характеристического уравнения (12.1) располагались в начале координат на плоскости z, т.е. Тогда передаточная функция замкнутой системы принимает вид

(12.19)

Пусть, например, степень полинома на единицу меньше степени характеристического полинома, т.е. равна Тогда выражение (12.19) примет вид

(12.20)

Передаточной функции (12.20) соответствует разностное уравнение вида (10.5)

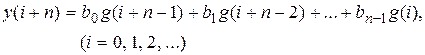
или разностное уравнение вида (10.6) .

При подаче на вход системы единичного ступенчатого воздействия 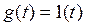и при 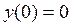получим:

Как видим переходный процесс заканчивается за конечное время

Следует однако учитывать, что системы с процессами конечной длительности часто имеют малый запас устойчивости. Например, в системе, рассмотренной в примере данного раздела, можно получить процесс с если При этом запас устойчивости замкнутой системы по амплитуде в соответствии с разделом 7.8 равен (см. рис. 12.2):

(12.21)

что является нижней границей рекомендуемого диапазона запаса устойчивости.