Понятие о z-преобразовании

Для последовательностей мгновенных импульсов вида (9.4)

может быть введено понятие дискретного преобразования Лапласа, определяемое формулой

(11.1)

Определяя каждый интеграл в выражении (11.1) по аналогии с (9.9), приведём (11.1) к виду:

F(s)= (11.2)

Введём новую комплексную переменную, аналогичную переменной (10.12):

(11.3)

Тогда выражение(11.2) принимает вид:

(11.4)

Функцию F(z) называют z-преобразованием сигнала f(t). Часто формулу(11.4) записывают, опуская обозначение периода дискретности как аргумента функции f(t):

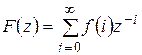(11.5)

Формулу преобразования (11.5) можно записать в символической форме:

F(z)=Z[f(i)] или F(z)=Z[f(t)], t=iT, i=0,1,2,… (11.6)

Пример. Определить z-преобразование сигнала x(t)=1(t).

Решение. В соответствии с (11.5)

Видно, что X(z) есть сумма бесконечной геометрической прогрессии, первый член которой а₀=1, а знаменатель прогрессии q=z^-1. Сумма (n+1) членов прогрессии равна

следовательно,

(11.7)

Рассмотрим некоторые правила и теоремы применительно к z-преобразованию.

1.Свойство линейности.

Изображение линейной комбинации последовательностей равно той же линейной комбинации их изображений.

Пусть f(i)= . (11.8)

Тогда для изображения можно записать

F(z)= . (11.9)

2.Теорема запаздывания и упреждения.

Рассмотрим последовательность f(i-m), сдвинутую вправо (запаздывающую) на целое число тактов m. Тогда из формул (11.5), (11.6) следует

Z[f(i-m)]= 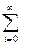f(i-m)z ^-i . (11.10)

Обозначим в формуле (11.10) r=i-m.Тогда i=r+m, при i=0 r=-m, при , а формула (11.10) примет вид:

(11.11)

Здесь F(z)=Z[f(i)]. Если исходная последовательность f(i) равна нулю при отрицательных значениях аргумента (нулевые начальные условия), то формула(11.11) упрощается:

Z[f(i-m)]=z ^-mF(z). (11.12)

Если сдвиг происходит влево (упреждение) и рассматривается последовательность f(i+m), где m-целое положительное число, то аналогично случаю запаздывания можно показать, что

(11.13)

Второе слагаемое в правой части(11.13) обращается в нуль, если f(i)=0 при i=0,1,...,m-1.

3.Сумма ординат последовательности.

Формула z-преобразования (11.5) при (что соответствует условию ) даёт сумму ординат последовательности f(i):

F(1)= (11.14)

4. Конечное значение последовательности.

Составим первую прямую разность последовательности f(i) и на основании (11.9) найдём её изображение

Z[∆f(i)]=Z[f(i+1)-f(i)]=Z[f(i+1)]-Z[f(i)]=z[F(z)-f(0)]-F(z)=

=(z-1)F(z)-zf(0).

Далее на основании (11.14) найдём сумму ординат ∆f(i):

(11.15)

Кроме того, можно записать, что сумма ординат ∆f(i) есть разность между значением f(i) при i и начальной ординатой f(0):

(11.16)

Значение f(i) при i есть конечное значение последовательности. Из двух последних выражений следует:

(11.17)

Пример. Определить конечное значение выходной величины y(i) импульсной системы, описываемой разностным уравнением (10.9), при начальных условиях y(-1)=y(-2)=0 и единичной входной последовательности u(t)=1(t), т.е. u(0)=u(1)=...=1, u(i)=0 при i<0.

Решение. Применим к разностному уравнению (10.9) z‑преобразование и на основании свойства линейности получим выражение

Z[y(i)] - 0,27 Z[y(i-1)] + 0,135 Z[y(i-2)] = 0,865 Z[u(i-1)], (11.18)

где Z[y(i)]=Y(z);

Z[y(i-1)]=z ^-1[Y(z)+y(-1)z]=z ^-1Y(z);

Z[y(i-2)]=z ^-2[Y(z)+y(-1)z+y(-2)z²]=z ^-2Y(z);

Z[u(i-1)]=z ^-1[U(z)+u(-1)z]=z ^-1U(z) .

В соответствии с (11.7) изображение единичной последовательности

Z[u(i)]=U(z)= .

Из уравнения (11.18) определим изображение выходной величины:

Y(z)=

Конечное (установившееся) значение выходной величины найдём по формуле (11.17):

.