Решение разностных уравнений

Разностные уравнения по существу являются рекуррентными соотношениями, позволяющими при последовательно шаг за шагом (т.е. рекуррентно) вычислять значения выходной величины при заданных ее начальных значениях и любых заданных аналитически, графически или таблично значениях входной величины

Выразим из уравнения (10.6) текущее значение выходной величины

(10.7)

Значения выходной величины являются предыдущими по отношению к текущему значению y(k). Так как временной интервал поиска решения уравнения (10.7) начинается со значения k=0 (t₀=0), то величины должны быть заданы как начальные значения, например, y(i)=0 при i<0. Тогда при заданных значениях входной величины u(i) из уравнения (10.7) можно последовательно найти y(0), y(1), y(2),…

Пример 1.Найти значения y(k), k=0, 1, 2, 3,…для разностного уравнения

y(i+2)-0,27y(i+1)+0,135y(i)=0,865u(i+1) (10.8)

При начальных значениях y(k)=0 при k<0 и единичной входной последовательности u(0)=u(1)=…=1, u(k)=0 при k<0.

Решение. Приведём уравнение (10.8) к виду (10.7):

y(i)=0,27y(i-1)-0,135y(i-2)+0,865u(i-1). (10.9)

Используя начальные условия, получим:

и так далее.

Общее решение неоднородного разностного уравнения (10.5) и (10.6) представляется в виде суммы переходной и вынужденной составляющих. Переходная составляющая, т.е. общее решение однородного уравнения

(10.10)

определяется по аналогии с решением дифференциального уравнения в виде

(10.11)

Введем новую комплексную переменную

. (10.12)

Подставим (10.12) в выражение (10.11) и, опуская для упрощения записи параметр Т, получим решение однородного разностного уравнения в виде

, (10.13)

где С – константа, зависящая от начальных условий.

Подставим решение (10.13) в однородное уравнение (3.23):

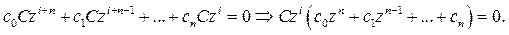(10.14)

Из выражения (10.14) следует, что

(10.15)

Решая характеристическое уравнение (10.15), найдем корни Если 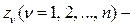некратные корни характеристического уравнения, то переходная составляющая общего решения неоднородного разностного уравнения

(10.16)

Из (10.16), в частности, вытекает условие затухания свободного движения системы, описываемой разностным уравнением (10.5), т.е. условие устойчивости:

(10.17)

Вынужденную составляющую определяют по виду правой части уравнения (10.5).

Пример 2. Найти общее решение неоднородного разностного уравнения (10.8). Решение. Характеристическое уравнение имеет пару комплексно-сопряженных корней

где

Так как условие (10.17) выполняется, система устойчива.

Общее решение однородного уравнения (переходная или свободная составляющая ) имеет вид:

(10.18)

Вынужденную составляющую y_В ищем по виду правой части уравнения (10.8), значения которой с течением времени не изменяются. Это значит, что после затухания переходной составляющей (10.18) при значения выходной переменной будут оставаться неизменными и равными вынужденной составляющей y_В, т.е. при . Так как , то из (10.8) получим вынужденную составляющую в виде:

(10.19)

Общее решение неоднородного уравнения (10.8) получим, сложив выражения (10.19) и (10.18):

(10.20)

Чтобы найти константы и 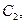вычислим значения y(0) и y(1) из уравнения (10.8): y(0)=0, y(1)=0,865.

Подставляя значения y(0)=0, y(1)=0,865 в (10.20), получим уравнения

из которых найдем C₁=C₂=-0,5.

Искомое решение получим в виде:

(10.21)

Подставляя в (10.21) значения i=0,1,2,…, получим тот же ряд значений y(i) (табл.10.1), что и при рекуррентном вычислении по формуле (10.9).

Таблица 10.1

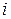
		0,865	1,0985	1,0448	0,9988	0,9936	0,9984	1,0004