Тема 10. Разностные уравнения импульсных систем

10.1. Основные понятия о разностных уравнениях

Будем полагать, что входным сигналом системы, приведенной на рис.9.2, является не а последовательность 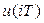мгновенных значений непрерывной функции В качестве выходного сигнала системы будем рассматривать последовательность y(iT) мгновенных значений непрерывного сигнала y(t). Условно это отображено на рис. 10.1. наличием ключа на выходе непрерывной части.

Часто оказывается удобным считать расстояния между дискретными значениями функции равным единице. При этом вводится понятие об относительной переменной времени 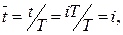а решетчатая функция представляется в виде функции

Скорость изменения решетчатой функции характеризуется разностью первого порядка, которая является аналогом производной
непрерывной функции времени. Разность первого порядка (первая разность) для любой последовательности f(i) определяется в момент времени 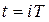как разность между будущим значением последовательности при и текущим значением при t=iT:

(10.1)

Аналогом второй производной непрерывной функции для последовательности является конечная разность второго порядка или вторая разность

(10.2)

Разность -го порядка определяется рекуррентным соотношением или в общем виде

(10.3)

где - биноминальные коэффициенты.

В качестве аналога дифференциального уравнения можно рассматривать уравнение в конечных разностях

(10.4)

где

Однако при исследовании дискретных систем удобнее пользоваться уравнением

(10.5)

которое получается из (10.4) с учетом (10.3). Оно и называется разностным уравнением.

Если ввести новую переменную времени 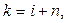то уравнение (10.5) можно представить в виде

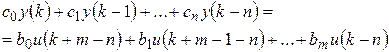(10.6)

более удобном для пошагового вычисления значений выходной величины при