
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Составление разностных уравнений импульсной системы
Запишем разностные уравнения разомкнутой импульсной системы, структурная схема которой показана на рис.10.1. Подобные системы называют импульсными фильтрами. Непрерывная часть и формирующее устройство образуют приведенную непрерывную часть (ПНЧ) импульсного фильтра, на вход которого подаются мгновенные импульсы (рис.10.2).
Рассмотрим один из способов получения разностных уравнений, основанный на решении дифференциальных уравнений непрерывной части фильтра в интервале iT£t<(i+1)T. При этом значения выходной величины y(i), y(i-1),… рассматриваются как начальные условия. При подстановке в найденное решение y(t), t =t-iT предельного значения t =Т получим дискрету y(i+1).
Пример. Записать разностное уравнение разомкнутого дальномера с одним интегратором, широко применяемого в радиолокационных станциях. Передаточная функция интегратора W0(s)=k/s.
Решение. Разностное уравнение формирователя, устанавливающее связь между последовательностями сигналов u*(t)=u(i) и ut*(t), имеет вид:
ut*(i)= u(i). (10.22)
Дифференциальное уравнение непрерывной части определяет зависимость выходного сигнала y(t) от сигнала на входе НЧ ut*(t):
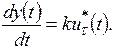 (10.23)
(10.23)
Найдем решение уравнения (10.23) на интервале времени iT £t£ (i+1)T, когда ut*(t)= u(i)1(t-iT).

Уравнение (10.24) и есть искомое разностное уравнение, которое можно записать также в форме (10.6):

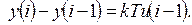 (10.25)
(10.25)
Дата добавления: 2014-11-13; просмотров: 356; Мы поможем в написании вашей работы!; Нарушение авторских прав |