Вывод уравнений импульсного элемента

Рассмотрим разомкнутую систему, состоящую из импульсного элемента и непрерывной части (рис 9.2). Импульсный элемент на рис. 9.2 условно заменён последовательным соединением ключа и формирующего устройства с передаточной функцией W_ф, непрерывная часть представлена звеном с передаточной функцией W_o. Ключ периодически с периодом Т замыкается на очень короткий промежуток времени и выделяет из непрерывного сигнала u(t) его мгновенные значения u(iT):

(9.2)

Последовательности типа u(iT) (или в сокращённой записи u(i) ), (i=0,1,2,…) называют решётчатыми функциями, а ординаты u(iT) - дискретами решётчатой функции. Формирующее устройство преобразует последовательность u(iT), (i=0,1,2…) в прямоугольные импульсы длительностью в соответствии с выражением (9.1). Коэффициент пропорциональности k_А можно отнести к непрерывной части системы. Тогда амплитуда (высота) импульсов будет равна u(iT):

(9.3)

Передаточная функция W_ф(s) может быть определена как отношение изображений по Лапласу выходной величины формирующего устройства и его входной величины. Однако входная величина представляет собой последовательность u(iT), для которой преобразование Лапласа не существует. Чтобы устранить эту неопределённость, положим, что идеальный импульсный элемент (ключ) генерирует не импульсы конечной высоты u(iT), а бесконечно короткие по длительности импульсы типа d‑функций, площади которых пропорциональны значениям u(iT). В этом случае математическую модель дискретной последовательности u^*(t) можно представить выражением:

(9.4)

Отдельный импульс последовательности (9.4) в произвольный момент времени kТ определяется выражением:

. (9.5)

Чтобы найти площадь мгновенного импульса, надо проинтегрировать функцию (9.5) по времени от нуля до бесконечности. Площадь S(kT) импульса u^* в силу фильтрующего свойства δ – функции равна u(kT).

При поступлении на вход формирующего устройства единственной дискреты u(kT), которая формально заменяется δ - функцией (9.5), на его выходе образуется прямоугольный импульс высотой u(kT) и длительностью :

(9.6)

Для отыскания изображения входного сигнала (9.5) по Лапласу

(9.7)

введём новую переменную интегрирования:

(9.8)

Выполним замену переменной интегрирования в (9.7):

(9.9)

Интервал ∆x=[0^-;0] есть время действия импульса δ(x). Значение x=0^- бесконечно близко значению x=0.

Применим прямое преобразование Лапласа к выходному сигналу (3.6):

(9.10)

Если в первом интеграле (9.10) выполнить замену переменной интегрирования в соответствии с выражением (9.8), а во втором ввести новую переменную интегрирования x^’=t-(k+ )T, то получим изображение выходного сигнала в виде:

. (9.11)

Поделив изображение выхода (9.11) на изображение входа (9.9), получим передаточную функцию формирующего устройства:

(9.12)

В системах автоматического управления преимущественно используются формирующие устройства, удерживающие на выходе величину, равную в течение всего периода дискретности В этом случае а само формирующее устройство называется экстраполятором нулевого порядка. Передаточная функция (9.12) при 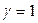принимает вид

(9.13)