Оценка качества переходного процесса по логарифмическим частотным характеристикам разомкнутой системы

Рассмотрим связь между переходными характеристиками и ЛАХ для систем первого и второго порядка.

Пример 1. Система состоит из интегрирующего звена, охваченного жесткой отрицательной обратной связью (рис. 8.4 а)

Элементарная замкнутая система в этом случае представляет собой инерционное (апериодическое) звено:

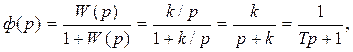(8.12)

где 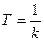- постоянная времени.

Разомкнем обратную связь и построим ЛАХ разомкнутой системы:

При 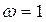значение 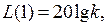а при 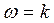получаем 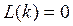(рис. 8.4 б). Частота 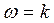есть частота среза .

Дифференциальное уравнение замкнутой системы получим на основании ее передаточной функции (8.12):

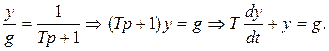
Реакция замкнутой системы на входное воздействие g(t)=1(t) при нулевых начальных условиях (y(0)=0) есть переходная характеристика системы (см. (4.36) при k=1), приведенная на рис. 4.7:

Время переходного процесса для экспоненциальной кривой обычно принимается равным 3Т (время входа переходной характеристики в пятипроцентную трубку), поэтому

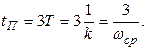(8.13)

На основании (8.13) заключаем, что время переходного процесса замкнутой системы первого порядка определяется частотой среза 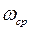разомкнутой системы.

Пример 2. Для системы второго порядка, содержащей интегрирующее и инерционное звенья (рис. 8.5 а), передаточная функция разомкнутой системы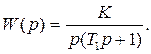

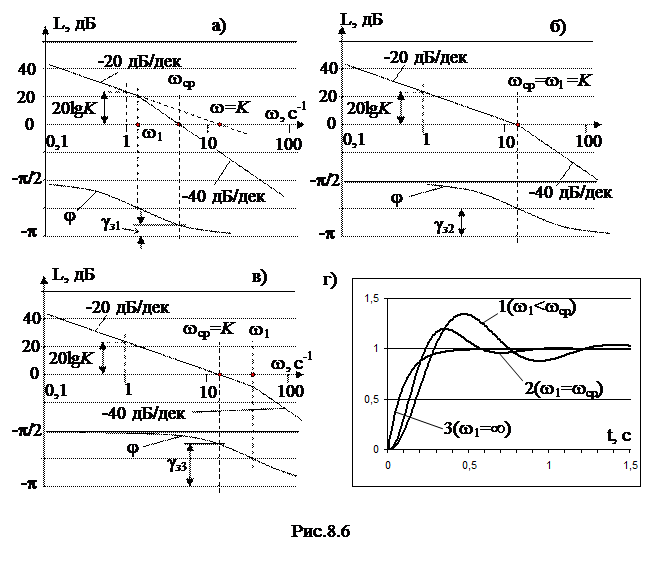
ЛАХ разомкнутой системы содержит три составляющие: безынерционного 1, интегрирующего 2 и инерционного 3 звеньев (рис. 8.5 б): 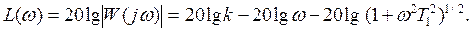При различном соотношении параметров звеньев результирующая ЛАХ разомкнутой системы будет иметь различный вид (рис. 8.6 а; 8.6 б; 8.6 в). На рис. 8.6 а показан вариант, когда частота сопряжения 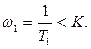В этом случае ЛАХ пересекает ось частот в точке 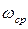с наклоном –40 дБ/дек и система имеет небольшой запас устойчивости по фазе . С уменьшением постоянной времени T₁ частота w₁ возрастает, и точка излома асимптотической ЛАХ сдвигается вправо. На рис. 8.6 б частота . При этом заметно вырос запас устойчивости системы по фазе 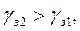а в случае 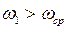(рис. 8.6 в) имеем запас устойчивости по фазе Запишем передаточную функцию замкнутой системы:

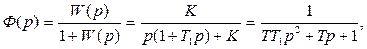(8.14)

где - постоянная времени.

Выразим передаточную функцию (8.14) через коэффициент демпфирования z и через собственную частоту колебаний w₀:

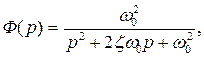
где

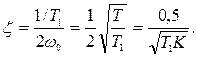
Чем меньше T₁ (большеw₁), тем больше значение коэффициента демпфирования z (больше запас устойчивости системы по фазе ). Для различных соотношений частот w₁ и w_ср соответственно виду ЛАХ (см. рис. 8.6 а, б, в) переходные характеристики замкнутой системы при 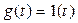приведены на рис. 8.6 г. В случае 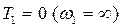вместо (8.14) получим выражение, аналогичное (8.12), когда переходный процесс в системе является апериодическим (кривая 3 на рис. 8.6 г).

Практически установлено, что при 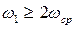переходный процесс замкнутой системы второго порядка будет без перерегулирования, а его время может приближенно определяться равенством (8.13).

В результате исследования автоматических систем с различным видом ЛАХ установлено, что колебательность переходного процесса будет наименьшей, если частота среза разомкнутой системы находится на участке ЛАХ с наклоном –20 дБ/дек. Для систем высокого порядка при этом время переходного процесса определяется неравенством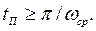

Если переходный процесс в системе заканчивается за 1-2 колебания, то время переходного процесса можно определить по приближенной зависимости 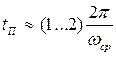. (8.15)

Чем шире участок ЛАХ с наклоном -20 дБ/дек, пересекающий ось абсцисс, тем ближе переходная характеристика к экспоненте.

В общем случае ЛАХ разомкнутой системы имеет произвольный вид. Однако, как показали исследования, вид участка ЛАХ при низких частотах мало влияет на характер переходного процесса. Низкочастотный участок ЛАХ характеризует ошибку автоматических систем (см. рис. 8.2). Следовательно, при оценке переходного процесса по ЛАХ разомкнутой системы низкочастотный участок можно не учитывать. Аналогичный вывод можно получить относительно участка ЛАХ, соответствующего высоким частотам.