Точность в типовых режимах

Для оценки точности системы управления используется величина ошибки в различных типовых режимах

Величину ошибки можно определить выражением, полученным в разделе 5.3:

(8.5)

Чтобы найти установившееся значение ошибки , воспользуемся теоремой о конечном значении:

(8.6)

Первое слагаемое представляет собой составляющую установившейся ошибки от задающего воздействия, а второе - от возмущающего воздействия.

Входящая в выражение (8.6) передаточная функция разомкнутой системы W(s) может быть представлена в виде

где K – коэффициент передачи (усиления) разомкнутой системы; -составляющая передаточной функции 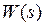, не содержащая интегрирующих или идеальных дифференцирующих звеньев и равная 1 при s=0; r - число интегрирующих звеньев, входящих последовательно в разомкнутую цепь системы. При r=0 система называется статической, а при - астатической. Величина r определяет порядок астатизма системы.

Рассмотрим наиболее употребительные режимы.

1.Неподвижное состояние. В качестве типового режима рассматривается установившееся состояние при постоянных значениях задающего и возмущающего воздействий. Примем, что задающее и возмущающее воздействия в момент времени t=0 изменяются от нуля до постоянных значений

В этом случае изображения внешних воздействий по Лапласу определяются формулами:

(8.7)

Докажем справедливость формул (8.7) на примере преобразования по Лапласу задающего воздействия где при и при .

Заметим, что первое слагаемое в скобках (8.8) обращается в ноль при в случае, если вещественная часть комплексной переменной называемая абсциссой абсолютной сходимости, положительна (см. раздел 2.2.2).

Подставляя (8.7) в формулу (8.6), определим величину ошибки, которая в этом случае называется статической:

.

В статических системах Тогда статическая ошибка от задающего воздействия

В астатических системах , поэтому составляющая . Однако это ещё не означает, что вторая составляющая в астатических системах также равна нулю, так как возможен случай, когда .

2. Движение с постоянной скоростью. В качестве второго типового режима используется режим движения с постоянной скоростью , который будет наблюдаться в установившемся состоянии при задающем воздействии, изменяющемся по закону , и при постоянном значении возмущающего воздействия .

Найдем изображение задающего воздействия по Лапласу, применив способ интегрирования по частям.

Из общего выражения для ошибки (8.6) найдем установившуюся ошибку

(8.9)

Первое слагаемое (8.9) имеет смысл только при астатизме первого порядка, т.е. в том случае, когда передаточная функция разомкнутой системы может быть представлена в виде где K - коэффициент передачи разомкнутой системы, называемый в данном случае добротностью по скорости. Тогда выражение (8.9) приводится к виду

Таким образом, в этом типовом режиме установившаяся ошибка будет слагаться из статической ошибки

и добавочной скоростной ошибки х_с, равной отношению заданной скорости к добротности системы по скорости х_с=v/K.

В статических системах первое слагаемое (8.9) стремится к бесконечности, при астатизме выше первого порядка это слагаемое стремится к нулю. На рис. 8.1 показаны примеры переходных процессов для статической системы (рис. 8.1 а) и системы с астатизмом первого порядка (рис. 8.1 б) .

3. Движение по гармоническому (синусоидальному) закону.