
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Принцип аргумента
Рассмотрим алгебраическое уравнение n-й степени с действительными коэффициентами: 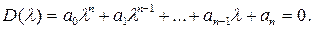
Если через  обозначить корни этого уравнения, то многочлен
обозначить корни этого уравнения, то многочлен 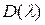 можно представить в виде произведения простых сомножителей:
можно представить в виде произведения простых сомножителей: 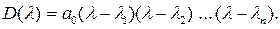
На комплексной плоскости  каждому корню соответствует вполне определенная точка. Геометрически каждый корень
каждому корню соответствует вполне определенная точка. Геометрически каждый корень  можно изобразить в виде вектора, проведенного из начала координат к точке (
можно изобразить в виде вектора, проведенного из начала координат к точке (  где
где 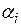 - вещественная часть корня
- вещественная часть корня  , а
, а 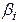 - мнимая (рис. 7.1 а).
- мнимая (рис. 7.1 а).
Если положить  в
в 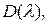 то
то
 (7.23)
(7.23)
 Изобразим на комплексной плоскости элементарный вектор
Изобразим на комплексной плоскости элементарный вектор  (рис. 7.1 б). Этот вектор является разностью двух векторов: вектора
(рис. 7.1 б). Этот вектор является разностью двух векторов: вектора  и вектора
и вектора  Концы элементарных векторов
Концы элементарных векторов  находятся на мнимой оси в точке
находятся на мнимой оси в точке  , а начала – в точках с координатами
, а начала – в точках с координатами 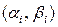 . При изменении w от 0 до ¥ концы векторов
. При изменении w от 0 до ¥ концы векторов  скользят по мнимой оси, а векторы
скользят по мнимой оси, а векторы  при этом поворачиваются. Направление вращения вектора против часовой стрелки с ростом
при этом поворачиваются. Направление вращения вектора против часовой стрелки с ростом  принимают за положительное. Если начало вектора
принимают за положительное. Если начало вектора  лежит в левой части комплексной плоскости (вещественная часть корня li отрицательная), то при изменении w от 0 до ¥ вектор
лежит в левой части комплексной плоскости (вещественная часть корня li отрицательная), то при изменении w от 0 до ¥ вектор  вращается в положительную сторону и изменение его аргумента
вращается в положительную сторону и изменение его аргумента
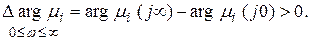
Для всех корней 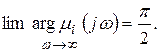
Начальные значения аргументов векторов  различны в зависимости от четырёх возможных вариантов расположения корней на комплексной плоскости (рис. 7.2). Найдем изменение аргумента элементарных векторов
различны в зависимости от четырёх возможных вариантов расположения корней на комплексной плоскости (рис. 7.2). Найдем изменение аргумента элементарных векторов  при изменении w от 0 до
при изменении w от 0 до  для приведённых на рис.7.2 вариантов расположения корней.
для приведённых на рис.7.2 вариантов расположения корней.

Вариант 1. Вещественный корень в левой части КП.
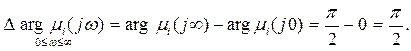
Вариант 2. Вещественный корень в правой части КП.
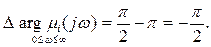
Вариант 3. Пара комплексно-сопряженных корней в левой части КП.


Векторы  и
и  запишем в показательной форме:
запишем в показательной форме:

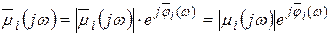 ,
,
где 
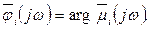
В выражении для полинома  векторы
векторы  и
и  являются сомножителями. Запишем формулу для произведения векторов
являются сомножителями. Запишем формулу для произведения векторов  и
и  :
: 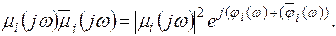
Найдем изменение аргумента произведения векторов  и
и  при изменении w от 0 до
при изменении w от 0 до  :
:
 .
.
Вариант 4. Пара комплексно-сопряженных корней в правой части КП.

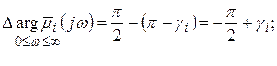
По аналогии вариантом 3 найдем изменение аргумента произведения векторов  и
и  при изменении w от 0 до
при изменении w от 0 до  :
:
 .
.
Запишем выражение для вектора 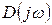 (см. (7.23)).
(см. (7.23)).
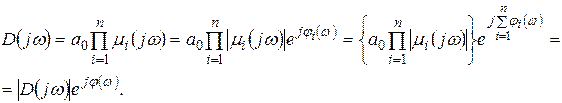
Аргумент (или фаза) вектора  равен сумме аргументов элементарных векторов:
равен сумме аргументов элементарных векторов: 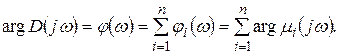
Предположим, что уравнение  =0 имеет m корней в правой части КП и, следовательно, n-m корней в левой части КП. Пусть при этом q правых корней и r левых корней – вещественные. Тогда в правой части КП количество пар комплексно-сопряженных корней будет равно (m-q)/2 а в левой (n-m-r)/2 При возрастании w от 0 до
=0 имеет m корней в правой части КП и, следовательно, n-m корней в левой части КП. Пусть при этом q правых корней и r левых корней – вещественные. Тогда в правой части КП количество пар комплексно-сопряженных корней будет равно (m-q)/2 а в левой (n-m-r)/2 При возрастании w от 0 до  изменение аргумента вектора
изменение аргумента вектора 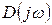 или угол поворота
или угол поворота 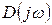 будет
будет

Если все корни уравнения  =0 находятся в левой части КП, то
=0 находятся в левой части КП, то
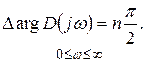
Дата добавления: 2014-11-13; просмотров: 365; Мы поможем в написании вашей работы!; Нарушение авторских прав |