Тема 7. Устойчивость линейных непрерывных САУ

Основные понятия об устойчивости

Пусть уравнения состояния системы, характеризующие ее свободное движение, представлены системой нелинейных дифференциальных уравнений

(7.1)

где - обобщенные координаты системы, т.е. переменные, описывающие ее состояние;

- известные функции, определенные в некоторой фиксированной области пространства переменных .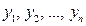

Пусть величины обозначают начальные значения переменных 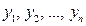.Каждой системе начальных значений соответствует решение уравнений (7.1)

(7.2)

Среди решений (7.2) имеется так называемое очевидное решение уравнений (7.1), характеризующее установившийся процесс, когда переменные состояния принимают постоянные значения

(7.3)

Если подставить решение (7.3) в дифференциальные уравнения (7.1), то левые части уравнений обратятся в ноль. Тогда решение (7.3) можно получить как корни уравнений

(7.4)

Решение (7.3) входит в семейство решений (7.2) и определяется начальными условиями (7.5)

Введем отклонения координат от установившихся значений:

(7.6)

Подставляя в уравнения (7.1) значения обобщенных координат

получим:

(7.7)

Так как постоянные величины, в правой части уравнения (7.7) записана функция переменных :

; (7.8)

Подставив обозначения (7.8) в уравнения (7.7), получим уравнения возмущенного движения:

(7.9)

Формула (7.6) определяет преобразование переноса начала координат в точку

(7.10)

Решению (7.3) в пространстве координат соответствует решение (7.11)

По терминологии А.М. Ляпунова уравнения (7.11) называют невозмущенным движением системы.

При переменные принимают начальные значения , которые называют возмущениями. Каждой заданной системе таких возмущений отвечает однозначное и непрерывное решение уравнений (7.9). Это решение называют возмущенным движением системы.

В большинстве задач теории автоматического управления функции допускают разложение в степенные ряды, сходящиеся в некоторой H-окрестности начала координат (7.11):

если достаточно мала. В этих случаях уравнениям (7.9) можно придать вид

(7.12)

где 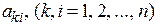- постоянные коэффициенты, полученные как значения частных производных функций по переменным , вычисленные при нулевых значениях переменных; функции, содержащие члены второго и выше порядка малости.

На практике судят об устойчивости решения (7.11), рассматривая лишь уравнения, называемые уравнениями 1-го приближения вместо уравнений (7.12):

(7.13)

А.М. Ляпунов показал, что все случаи исследования уравнений (7.13) следует разделять на категории некритических и критических случаев. К категории некритических относятся случаи, в которых вопрос об устойчивости (или неустойчивости) невозмущенного движения однозначно разрешается на основании исследования уравнений 1-го приближения (7.13).

Запишем уравнения (7.13) в векторно-матричной форме:

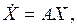(7.14)

где 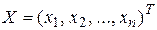- вектор состояния;

- квадратная матрица.

Характеристическое уравнение системы (7.13)

(7.15) приводится к виду

(7.16)

Пусть все корни уравнения (7.16) различны. Тогда решение уравнения (7.15) для переменной x_i имеет вид:

(7.17)

где - корни характеристического уравнения; - постоянные интегрирования, зависящие от начальных условий.

Пусть - вещественный корень. Если то член с течением времени непрерывно возрастает и стремится к бесконечности. В этом случае 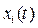также стремится к бесконечности и система неустойчива.

Если то член с течением времени стремится к нулю.

Пусть один из корней - комплексный, тогда всегда существует сопряженный с ним :

(7.18)

В этом случае константы интегрирования также будут комплексно-сопряженными величинами:

(7.19)

Составляющая решения (7.17), соответствующая корням (7.18), имеет вид:

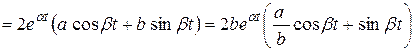(7.20)

Обозначим где j - угол фазового сдвига. Окончательно решение (7.20) примет вид:

(7.21)

Если то имеют место колебания с частотой и нарастающей амплитудой – движение неустойчиво.

Если получим незатухающие колебания – система на границе устойчивости.

Если то амплитуда колебаний с течением времени уменьшается – колебания затухают.

Отсюда можно сделать следующие выводы:

- если все вещественные части корней характеристического уравнения отрицательны, то система устойчива;

- если хотя бы один из корней имеет положительную вещественную часть, то система неустойчива.

- если среди корней характеристического уравнения имеется один или несколько нулевых корней, а вещественные части остальных корней отрицательны, то говорят, что система нейтрально устойчива. Этот случай называют критическим и для определения устойчивости системы требуется специальное исследование нелинейных членов разложения.