Преобразование структурных схем

Различные способы преобразования структурных схем облегчают определение передаточных функций сложных систем автоматического управления и дают возможность привести многоконтурную систему к эквивалентной ей одноконтурной.

Рассмотрим приведение к одному эквивалентному звену простейших сочетаний звеньев в структурных схемах.

а) Последовательное соединение звеньев (рис. 5.1)

Уравнения звеньев структурной схемы на рис. 5.1:

(5.1)

В результате взаимной подстановки выражений (5.1) получим уравнение эквивалентного звена (рис.5.2): x₄=W₃(p)W₂(p)W₁(p)x₁.

Нетрудно видеть, что передаточная функция эквивалентного звена W_э=W₃(p)W₂(p)W₁(p).

б) Параллельное соединение звеньев (рис. 5.3)

Запишем уравнения элементов схемы, приведенной на рис. 5.3.

. (5.2)

В результате исключения промежуточных переменных из уравнений (5.2) получим:

Таким образом, передаточная функция эквивалентного звена равна

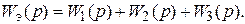
в) Встречно-параллельное соединение звеньев (обратная связь) (рис.5.4).

Обратная связь может быть положительной, если сигнал , снимаемый с выхода звена обратной связи, суммируется с сигналом на входе (рис. 5.4 а), и отрицательной, если вычитается (рис. 5.4 б).

Для определения передаточной функции эквивалентного звена запишем следующие очевидные соотношения:

(5.3)

где знак плюс относится к положительной обратной связи, а знак минус – к отрицательной обратной связи.

Исключим из выражений (5.3) переменную , подставив второе выражение в первое: 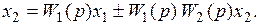(5.4)

Решив уравнение (5.4) относительно , найдем передаточную функцию эквивалентного звена

(5.5)

Здесь знак минус относится к положительной обратной связи, а знак плюс – к отрицательной обратной связи.

Если в одной из ветвей структурных схем, приведенных на рис. 5.4, нет звена (рис. 5.5), это означает, что передаточная функция данной ветви равна единице. Для варианта схемы, приведенной на рис. 5.5а, имеем Формула (5.5) для этого случая примет вид:

(5.6)

Для варианта схемы, приведенной на рис. 5.5 б, соответственно получим:

(5.7)