Запаздывающее звено

Уравнение запаздывающего звена 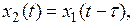(4.74)

где t - постоянное запаздывание.

Уравнение вида (4.74) называют уравнением с запаздывающим аргументом. Применим к уравнению (4.74) преобразование Лапласа.

(4.75)

Левый интеграл есть изображение выходной величины

(4.76)

Правый интеграл приведем к одному параметру интегрирования :

(4.77)

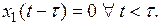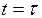
Первый интеграл в (4.77) равен нулю, т.к. Заменим во втором интеграле параметр интегрирования: . При при 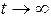. (4.78)

Подставляя (4.78) в (4.77), получим:

(4.79)

Подставляя в (4.75) выражения (4.76) и (4.79), окончательно получим: (4.80)

Передаточная функция запаздывающего звена

. (4.81)

Характеристики звена:

а) Переходная функция (4.82)

представляет собой единичную ступенчатую функцию, сдвинутую во времени относительно входного скачка на величину t.

б) Весовая функция точно также, как и переходная, повторяет входное воздействие с запаздыванием во времени на величину t:

в) Частотные характеристики звена определяются формулой

(4.83)

АЧХ запаздывающего звена ФЧХ:

АФХ представляет собой окружность единичного радиуса с центром в начале координат. При увеличении частоты вектор вращается по часовой стрелке.