
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дифференцирующее звено первого порядка
Дифференцирующее звено 1–го порядка имеет передаточную функцию вида
 (4.10)
(4.10)
где k – передаточный коэффициент звена; t – постоянная времени.
Уравнение этого звена
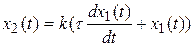 (4.11)
(4.11)
получим из (4.2) при  При этом
При этом 
 Выходная величина этого звена определяется не только текущим значением, но и скоростью изменения входной величины.
Выходная величина этого звена определяется не только текущим значением, но и скоростью изменения входной величины.
Характеристики звена:
а) Переходная функция определяется выражением
 (4.12)
(4.12)
При скачкообразном изменении входной величины 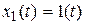 на выходе звена получим импульс с бесконечно большой амплитудой, соответствующий бесконечно большой скорости изменения входной величины в момент скачка. После этого выходная величина принимает постоянное установившееся значение
на выходе звена получим импульс с бесконечно большой амплитудой, соответствующий бесконечно большой скорости изменения входной величины в момент скачка. После этого выходная величина принимает постоянное установившееся значение  .
.
б) Частотные характеристики звена имеют вид:
 (4.13)
(4.13)
где 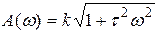 ,
, 
АФХ звена изображена на рис. 4.3. АФХ – прямая, параллельная мнимой оси. Она начинается на действительной оси в точке k при w=0.
Дифференцирующее звено создает опережение выходной величины по фазе. При  сдвиг по фазе стремится к 90°.
сдвиг по фазе стремится к 90°.
в) Уравнение ЛАХ:

 (4.14)
(4.14)
Для частот 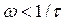 в выражении (4.14) можно пренебречь величиной
в выражении (4.14) можно пренебречь величиной 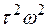 по сравнению с 1, а для частот
по сравнению с 1, а для частот  наоборот,
наоборот, 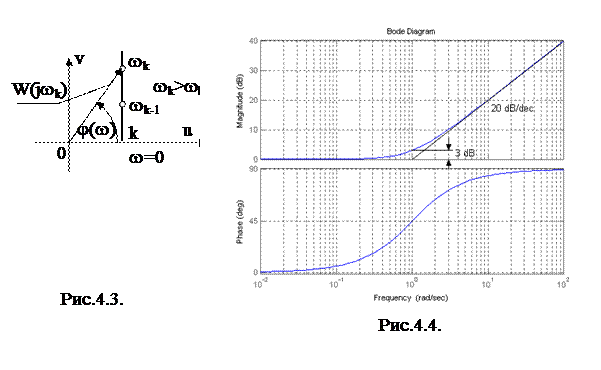 можно пренебречь единицей по сравнению с величиной
можно пренебречь единицей по сравнению с величиной  . Тогда приближенно можно записать
. Тогда приближенно можно записать
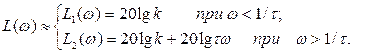 (4.15)
(4.15)
Соотношения (4.15) показывают, что ЛАХ дифференцирующего звена 1-го порядка приближенно может быть представлена двумя прямолинейными отрезками (асимптотами). В граничной точке 
 Действительное значение ЛАХ в точке
Действительное значение ЛАХ в точке 
 отличается от приближенного значения примерно на 3 дБ. Частота
отличается от приближенного значения примерно на 3 дБ. Частота  называется частотой сопряжения асимптотической ЛАХ. Линия
называется частотой сопряжения асимптотической ЛАХ. Линия 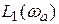 параллельна оси частот, а линия
параллельна оси частот, а линия 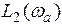 имеет положительный наклон +20 дБ/дек. На рис. 4.4 изображены ЛАХ и ЛФХ дифференцирующего звена 1-го порядка, построенные в зависимости от безразмерной (нормированной) частоты
имеет положительный наклон +20 дБ/дек. На рис. 4.4 изображены ЛАХ и ЛФХ дифференцирующего звена 1-го порядка, построенные в зависимости от безразмерной (нормированной) частоты  Нетрудно убедиться, что сопрягающей частотой будет значение
Нетрудно убедиться, что сопрягающей частотой будет значение 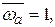 а ветвь
а ветвь 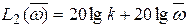 также будет иметь положительный наклон +20 дБ/дек. В логарифмическом масштабе частот характеристика
также будет иметь положительный наклон +20 дБ/дек. В логарифмическом масштабе частот характеристика 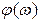 косо-симметрична относительно сопрягающей частоты
косо-симметрична относительно сопрягающей частоты 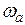 , при которой она имеет ординату 45°.
, при которой она имеет ординату 45°.
Дата добавления: 2014-11-13; просмотров: 318; Мы поможем в написании вашей работы!; Нарушение авторских прав |