Частотная передаточная функция и частотные характеристики

Пусть на входе динамического звена (рис.3.2) имеется гармоническое воздействие где - амплитуда, а w - угловая (круговая) частота этого воздействия.

На выходе линейного звена в установившемся режиме будет также гармоническая функция той же частоты, но в общем случае сдвинутая по фазе относительно входной величины на угол Y:

(3.7)

Воспользуемся формулой Эйлера

и представим входную и выходную величины в виде суммы экспоненциальных функций:

(3.8)

Дифференциальное уравнение звена запишем в виде

(3.9)

Выражения (3.8) есть частное решение дифференциального уравнения (3.9). В линейной системе на основании принципа суперпозиции эффект, создаваемый каждым из экспоненциальных воздействий и , может быть определен отдельно. Рассмотрим действие составляющей . Тогда

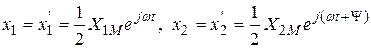(3.10)

Найдем производные функций (3.10):

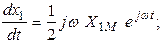
. (3.11)

Подставим значения входной и выходной величин и их производных в дифференциальное уравнение (3.9):

= (3.12)

После сокращения на общий множитель 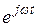найдем:

(3.13)

Выражение (3.14)

называется частотной передаточной функцией звена, которая представляет собой комплексное число. Выражение (3.14) можно представить в виде

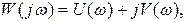(3.15)

где 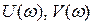- соответственно вещественная и мнимая частотные характеристики звена:

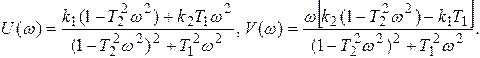(3.16)

Комплексное число можно выразить через его модуль и аргумент:

(3.17)

где амплитудная частотная характеристика звена;

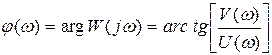- фазовая частотная характеристика звена.

Выражения (3.15) и (3.17) связаны между собой соотношениями

(3.18)

Сравнивая выражения (3.13) и (3.17), можно записать:

(3.19)

Таким образом, частотная передаточная функция представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной, а аргумент – сдвигу фаз выходной величины по отношению к входной.

Если рассмотреть действие составляющей , то соотношение между составляющими и 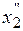получается таким же, как между 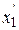и .

Для наглядного представления частотных свойств звена строится на комплексной плоскости его амплитудно-фазовая частотная характеристика (АФЧХ). Она представляет собой геометрическое место концов векторов (годограф), соответствующих частотной передаточной функции при изменении частоты от нуля до бесконечности (рис.3.3). По оси абсцисс откладывается вещественная часть и по оси ординат – мнимая часть Для каждой частоты на комплексной плоскости наносится точка. Полученные точки соединяются плавной кривой. Около нанесенных точек можно написать соответствующие им частоты 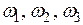и т.д.

Длина вектора, проведенного из начала координат в точку АФЧХ, соответствующую какой-то выбранной частоте, равна модулю частотной передаточной функции. Угол между вектором и положительным направлением вещественной оси, отсчитываемый против часовой стрелки, равен аргументу или фазе частотной передаточной функции.

Вместо АФЧХ можно построить отдельно амплитудно-частотную характеристику (АЧХ) и фазово-частотную характеристику (ФЧХ).

АЧХ показывает, как пропускает звено сигнал различной частоты. Оценка пропускания делается по отношению амплитуд выходной и входной величин. ФЧХ показывает фазовые сдвиги, вносимые звеном на различных частотах.