Определение передаточных функций через изображения Лапласа

Преобразованием Лапласа или изображением переменной x(t), такой, что и называется комплекснозначная функция 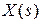, определяемая интегралом

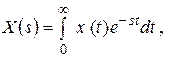(2.16)

где 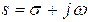- комплексная переменная, вещественная часть которой σ представляет собой так называемую абсциссу абсолютной сходимости. Для большинства функций, с которыми приходится иметь дело в управлении, абсцисса абсолютной сходимости равна нулю.

Функцию времени x(t) по которой найдено изображение 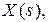называют оригиналом.

Отыскание изображения функции x(t) с помощью интеграла (2.16) называют прямым преобразованием Лапласа и условно обозначают его выражением

(2.17)

Умножим уравнение (2.8) на функцию и проинтегрируем его по времени от нуля до бесконечности.

Преобразование Лапласа обладает свойством линейности:

(2.18)

поэтому в левой и правой частях уравнения (2.8) будут суммы интегралов:

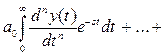
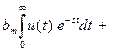
(2.19)

Согласно формуле (2.16) обозначим:

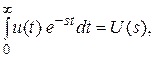
(2.20)

Найдем изображение первой производной.

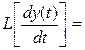
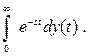(2.21)

Применим к (2.21) правило интегрирования по частям. Обозначим: 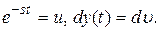Тогда (2.22)

Применяя такой же метод для нахождения изображения второй производной, получим формулу:

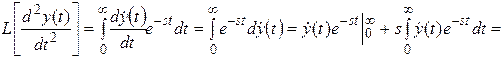
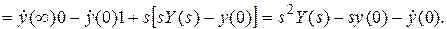(2.23)

Для изображения k - ой производной на основании формул (2.22) и (2.23) нетрудно найти выражение

(2.24)

Полагая все начальные условия нулевыми, запишем уравнение (2.19) в виде:

(2.25)