Символическая запись дифференциальных уравнений и передаточных функций

Уравнение (2.8) удобнее записывать в символической форме, вводя алгебраизированный оператор дифференцирования p=d/dt. Тогда любая производная уравнения (2.8) может быть выражена символьной формулой

(2.9)

а уравнение (2.8) примет вид:

(2.10)

Считая условно оператор дифференцирования p=d/dt алгебраической величиной, преобразуем уравнение (2.10) к виду:

(2.11)

где

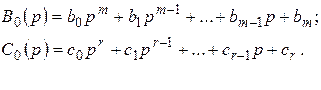
Полином A₀(p) представляет собой характеристический полином исследуемой системы (или её отдельного звена). Он характеризует свободное движение системы, т.е. её движение при u=0 и f=0 под влиянием ненулевых начальных значений вызванных, например, исчезнувшим к моменту времени t=0 возмущающим воздействием f(t). В зависимости от знаков вещественных частей корней уравнения A₀(p) система может быть устойчивой или неустойчивой.

Полином B₀(p) определяет влияние управляющего воздействия u(t) на характер изменения управляемой величины y(t).

Полином C₀(p) определяет влияние возмущающего воздействия f(t) на характер изменения управляемой величины.

Решим уравнение (2.11) относительно выходной величины:

(2.12)

Выражения

(2.13)

(2.14)

называются в теории автоматического управления передаточными функциями.

Выражения (2.10), (2.11), (2.12) представляют собой символическую запись дифференциального уравнения (2.8). Переменные в этих уравнениях остаются функциями времени. Чтобы подчеркнуть это, выражение (2.12) можно записать так:

(2.15)

Передаточные функции (2.13), (2.14) вводятся для сокращения символической записи дифференциальных уравнений. Более строго передаточная функция определяется через изображения Лапласа.