Линеаризация уравнений

Пусть динамическое уравнение некоторой САУ (или ее отдельного звена) имеет произвольный нелинейный вид

, (2.1)

где y – выходная величина; u – входная величина; f – внешнее возмущение; .

Допустим, что установившийся процесс в системе имеет место при некоторых постоянных значениях переменных u = u^*, f = f^*, y = y^*. Тогда уравнение установившегося состояния согласно (2.1) будет

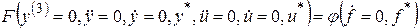(2.2)

В возмущенном движении переменные, являющиеся аргументами функций F и j уравнения (2.1), будут отличаться от своих установившихся значений:

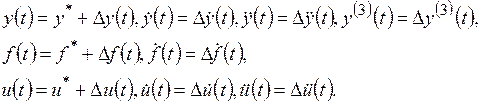(2.3)

В основе линеаризации нелинейных уравнений лежит предположение о том, что в исследуемом динамическом процессе переменные изменяются так, что их отклонения от установившихся значений, т.е. величины 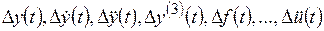, остаются все время достаточно малыми. Это допущение является справедливым в силу принципа работы замкнутой САУ.

Разложим функции F и j в уравнении (2.1) в ряд Тейлора по степеням указанных выше малых отклонений, рассматривая все производные тоже как самостоятельные переменные. Тогда уравнение (2.1) примет вид:

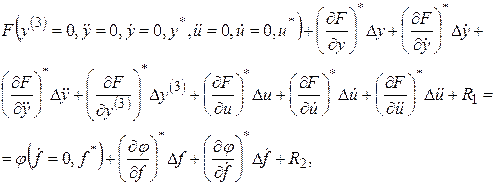(2.4)

где , например, означает частную производную 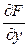, вычисленную при значениях переменных, соответствующих установившемуся режиму; R₁ – остаток ряда Тейлора для функции F, содержащий члены выше 1-го порядка малости; R₂ – остаток ряда Тейлора для функции j, содержащий члены выше 1-го порядка малости.

Вычтя из уравнения (2.4) уравнение установившегося состояния (2.2) и отбросив члены высшего порядка малости R₁ и R₂ , получим искомое линеаризованное уравнение динамики исследуемой системы в виде

(2.5)

Уравнение (2.5) называется дифференциальным уравнением системы (или ее отдельного звена) в отклонениях. Это уравнение записывают так, чтобы выходная величина и ее производные находились в левой части уравнения, а входная величина и все остальные члены – в правой части. Для коэффициентов уравнения (2.5) применим более простые обозначения

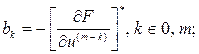
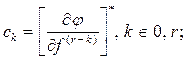(2.6)

где n, m, r – порядки старших производных выходной величины 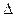y, входной величины 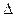u и возмущения 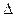f соответственно. С учетом обозначений (2.6) уравнение (2.5) примет вид:

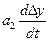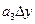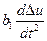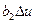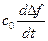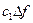+ + + = + + + + . (2.7)

Часто для упрощения записи знак вариации 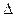в уравнении (2.7) опускают, не забывая при этом, что все переменные есть отклонения исходных величин от их установившихся значений. В общем случае уравнение (2.7) может быть записано в виде:

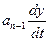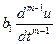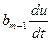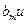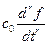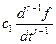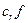+ +…+ + = + +…+ + + + + +…+ + . (2.8)

Для реальных систем обычно выполняется соотношение n>m, n>r.