Временные характеристики

Динамические свойства звена могут быть определены по его переходной функции и функции веса.

Переходная функция, или переходная характеристика, h(t) описывает переходный процесс на выходе звена, возникающий при подаче на его вход скачкообразного воздействия при величине скачка, равной единице. Такое входное воздействие называется ступенчатой единичной функцией и обозначается что соответствует х₁=0 при t<0 и х₁=1 при . Предполагается, что единица имеет ту же размерность, что и физическая величина на входе звена.

Если входное воздействие представляет собой неединичную ступенчатую функцию выходная величина будет равна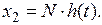

Умножение какой-либо функции времени x(t) на единичную ступенчатую функцию 1(t) означает, что функция времени x(t) будет существовать только при при t<0 она обращается в нуль.

Функция веса w(t) представляет собой реакцию звена на единичную импульсную функцию, поданную на его вход. Единичная импульсная функция или дельта–функция представляет собой производную от единичной ступенчатой функции:

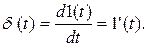(3.2)

Дельта-функция равна нулю повсюду, кроме точки t=0, где она стремится к бесконечности.

Основное свойство дельта - функции заключается в том, что

(3.3)

т.е. она имеет единичную площадь.

Установим связь между переходной функцией h(t) и функцией веса w(t). Рассмотрим входное воздействие в виде конечного по высоте N и ширине e импульса с площадью Ne=1, прикладываемого при t=0. Такой импульс может быть заменен двумя ступенчатыми функциями x₁₁=N×1(t) и x₁₂= -N×1(t-e), прикладываемыми ко входу звена со сдвигом во времени .

Тогда выходная величина будет равна

(3.4)

Будем теперь увеличивать высоту импульса N, одновременно уменьшая его ширину e, но так, чтобы все время Ne=1. Подставим N=1/e в (3.4)

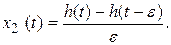
(3.5)

Переходя к пределу при , получим из (3.5) весовую функцию. С другой стороны, предел правой части выражения (3.5) есть скорость изменения переходной функции:

(3.6)

Таким образом, функция веса может быть получена дифференцированием по времени переходной функции.

В случае, если на вход звена поступает неединичная импульсная функция x₁=Gd(t), на выходе звена получим x₂=Gw(t).