Идеальное дифференцирующее звено

При уравнение (4.2) становится уравнением идеального дифференцирующего звена

(4.5)

где - передаточный коэффициент.

Передаточная функция звена W(p)=kp. В изображениях Лапласа при нулевых начальных условиях уравнение (4.5) примет вид

. (4.6)

Передаточная функция (4.7)

Идеальным дифференцирующим звеном можно моделировать, например, тахогенератор (ТГ), если в качестве входной величины ТГ выбрать угол поворота его ротора a, а в качестве выходной – напряжение , снимаемое с роторной обмотки (рис. 1.4).

Характеристики звена:

Для дифференцирующих звеньев из временных характеристик рассмотрим лишь переходную функцию.

а) Переходная функция есть импульсная функция, площадь которой равна k.

б) Частотная передаточная функция

(4.8)

где .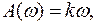

В соответствии с (3.28) при изменении частоты от 0 до (рис.4.1) конец вектора движется по положительной части мнимой оси от 0 до . Идеальное дифференцирующее звено создает опережение выходной величины по отношению к входной на 90^° на всех частотах. Амплитуда выходной величины возрастает с ростом частоты.

в) ЛАХ звена строим по уравнению

(4.9)

Выражение (4.9) есть уравнение прямой линии, которая имеет положительный наклон к оси с коэффициентом 20. Причем, если частота возрастает в 10 раз, т.е. на декаду, функция возрастает на 20 дБ. В этом случае говорят, что прямая (4.9) имеет наклон +20 дБ на декаду. На частоте 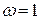прямая (4.9) проходит через точку (рис.4.2).