
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Апериодическое (инерционное) звено
Апериодическое звено имеет передаточную функцию 
 , (4.25)
, (4.25)
где k – передаточный коэффициент, T – постоянная времени.
Уравнение апериодического звена получим из (4.1) при 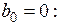
 (4.26)
(4.26)
где 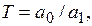

В качестве примера апериодического звена рассмотрим RC – цепочку (рис. 4.6). Входная величина RC–цепочки – напряжение U1, выходная – напряжение U2. По второму закону Кирхгофа
 (4.27)
(4.27)
где 
Выразим ток через напряжение на конденсаторе:
 . (4.28)
. (4.28)
Если исключить промежуточные переменные i и UR, то уравнение (4.27) примет вид
 (4.29)
(4.29)
который совпадает с (4.26) при k=1 и T=RC.
Запишем дифференциальное уравнение апериодического звена (4.26) в виде

 (4.30)
(4.30)
Решим уравнение (4.30) методом интегрирующего множителя, задав начальное условие  и полагая, что входное воздействие
и полагая, что входное воздействие  произвольная функция времени. Умножим правую и левую части уравнения (4.30) на вспомогательную функцию
произвольная функция времени. Умножим правую и левую части уравнения (4.30) на вспомогательную функцию 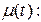
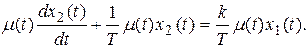 (4.31)
(4.31)
Подберем функцию  таким образом, чтобы в левой части уравнения (4.31) получилась производная от произведения
таким образом, чтобы в левой части уравнения (4.31) получилась производная от произведения

Для этого должно выполняться условие
 (4.32)
(4.32)
Решим уравнение (4.32) как дифференциальное уравнение с разделяющимися переменными:
 (4.33)
(4.33)
Подставив решение (4.33) в уравнение (4.31) и сократив последнее на 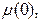 получим:
получим:
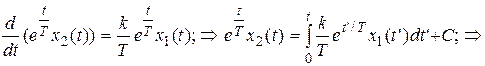
 (4.34)
(4.34)
С учетом начального условия  окончательно получим решение в виде
окончательно получим решение в виде
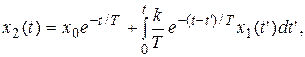 (4.35)
(4.35)
где t’ - переменная интегрирования.
Это полное решение уравнения (4.30) при произвольном воздействии. В нем можно выделить две составляющие: первая, зависящая от начального условия, является свободной составляющей; вторая носит название вынужденной составляющей. Используем решение (4.35) для получения переходной и весовой функций.
Характеристики звена:
а) Переходную функцию определяем при нулевом начальном условии и входном воздействии 

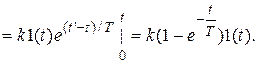 (4.36)
(4.36)
б) Прежде, чем найти весовую функцию, остановимся на одном важном свойстве  функции, которое называют фильтрующим. Рассмотрим интеграл от произведения
функции, которое называют фильтрующим. Рассмотрим интеграл от произведения  функции на гладкую функцию
функции на гладкую функцию  :
:
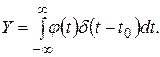 (4.37)
(4.37)
Функция  Примем, что импульс
Примем, что импульс 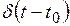 появляется в момент времени
появляется в момент времени  а заканчивается в момент времени
а заканчивается в момент времени  где
где 
 - бесконечно малая величина. С учётом этого запишем интеграл (4.37) как сумму трёх интегралов:
- бесконечно малая величина. С учётом этого запишем интеграл (4.37) как сумму трёх интегралов:
 (4.38)
(4.38)
Первый и третий интегралы в выражении (4.38) равны нулю в силу условия  а во втором интеграле
а во втором интеграле 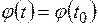 :
:
 (4.39)
(4.39)
Таким образом, получим, что интеграл от произведения гладкой функции  на функцию
на функцию 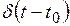 равен значению функции
равен значению функции  в момент времени существования
в момент времени существования  функции. Множитель
функции. Множитель  в выражении (4.39) отражает зависимость интеграла от времени.
в выражении (4.39) отражает зависимость интеграла от времени.
Весовую функцию апериодического звена ищем при нулевом начальном условии и входном воздействии  При подстановке входного воздействия в решение (4.35) запишем его в виде
При подстановке входного воздействия в решение (4.35) запишем его в виде  :
:
 (4.40)
(4.40)
Применим к решению (4.40) фильтрующее свойство  функции:
функции:
 (4.41)
(4.41)
Сравнивая выражение (4.41) с общим решением дифференциального уравнения апериодического звена (4.35), запишем последнее в виде:
 (4.42)
(4.42)
Интеграл вида (4.42) называется интегралом свертки функций  и
и  Графики переходной и весовой функций апериодического звена приведены на рис. 4.7.
Графики переходной и весовой функций апериодического звена приведены на рис. 4.7.
 г) Частотные характеристики апериодического звена могут быть получены из выражения для частотной передаточной функции
г) Частотные характеристики апериодического звена могут быть получены из выражения для частотной передаточной функции
 (4.43)
(4.43)
где 
АФХ апериодического звена при изменении частоты w от 0 до 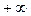 представляет собой полуокружность, диаметр которой равен передаточному коэффициенту k (рис. 4.8). При частотах
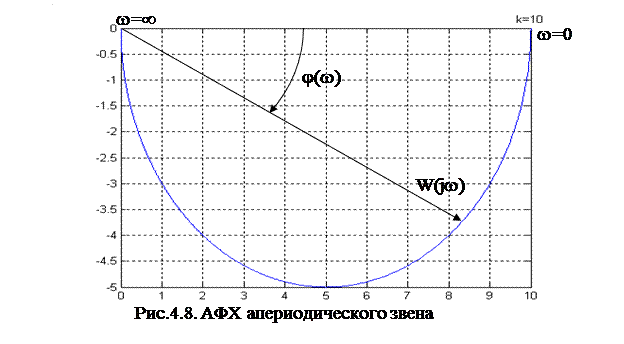
представляет собой полуокружность, диаметр которой равен передаточному коэффициенту k (рис. 4.8). При частотах 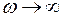 выходная величина отстаёт от входной на 900.
выходная величина отстаёт от входной на 900.
 д) Уравнение ЛАХ:
д) Уравнение ЛАХ: 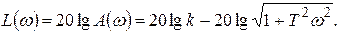 (4.44)
(4.44)
Сравнивая выражение (4.44) с уравнением ЛАХ дифференцирующего звена 1-ого порядка (4.15), можно сделать вывод, что ЛАХ апериодического звена есть зеркальное отображение ЛАХ дифференцирующего звена 1–ого порядка относительно горизонтальной асимптоты  ЛФХ апериодического звена есть зеркальное отображение ЛФХ дифференцирующего звена 1 – ого порядка относительного оси частот.
ЛФХ апериодического звена есть зеркальное отображение ЛФХ дифференцирующего звена 1 – ого порядка относительного оси частот.
На рис. 4.9 приведены графики ЛАХ и ЛФХ апериодического звена для случая k=10 в зависимости от нормированной частоты 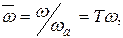 где
где  сопрягающая частота.
сопрягающая частота.

Дата добавления: 2014-11-13; просмотров: 410; Мы поможем в написании вашей работы!; Нарушение авторских прав |