Дифференцирующее звено второго порядка

Дифференцирующее звено 2-го порядка имеет передаточную функцию вида , (4.67)

где k – передаточный коэффициент, t_d – постоянная времени, x_d – коэффициент демпфирования.

Предполагается, что корни уравнения комплексно – сопряженные, т.е. выполняется условие .

Дифференциальное уравнение такого звена имеет вид

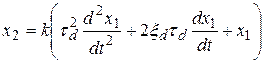и может быть получено из (4.45) при а₀=а₁=0. В этом случае

Характеристики звена:

а) Переходная характеристика

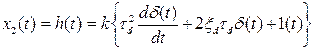. (4.68)

При скачкообразном изменении входной величины в момент времени t=0 на выходе получаются импульсы бесконечно большой амплитуды: 1) от 0 до ; 2) от до ; 3) от до

б) Частотные характеристики дифференцирующего звена второго порядка описываются формулой

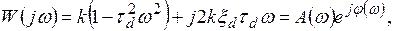(4.69)

где АЧХ: (4.70)

ФЧХ: (4.71)

АФХ звена представляет собой параболу

(4.72)

которая начинается из точки при (рис. 4.14).

Дифференцирующее звено второго порядка при частоте вносит опережение по фазе, стремящееся к 180⁰.

в) ЛАХ звена определяется формулой

(4.73)

Если сравнить формулу (4.73) с формулой (4.66) ЛАХ колебательного звена, то при и они отличаются друг от друга только знаком перед вторым слагаемым. Поэтому для дифференцирующего звена второго порядка кривая может быть получена как зеркальное отображение относительно прямой ЛАХ колебательного звена, а кривая ЛФХ может быть получена как зеркальное отображение относительно оси частот ЛФХ колебательного звена.