
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Обобщенная структурная схема и передаточные функции САУ
На рис. 5.6 приведена обобщенная структурная схема замкнутой системы автоматического управления.
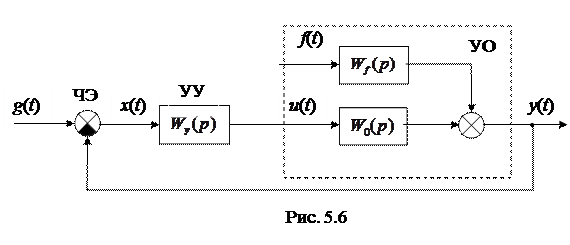 Обозначения на рис. 5.6: ЧЭ – чувствительный элемент; УУ – управляющее устройство; УО – управляемый объект;
Обозначения на рис. 5.6: ЧЭ – чувствительный элемент; УУ – управляющее устройство; УО – управляемый объект;  – управляемая величина;
– управляемая величина;  - задающее воздействие;
- задающее воздействие; 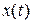 - рассогласование на выходе ЧЭ (ошибка управления);
- рассогласование на выходе ЧЭ (ошибка управления);  - управляющее воздействие;
- управляющее воздействие; 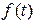 - возмущающее воздействие;
- возмущающее воздействие;  - передаточная функция управляющего устройства;
- передаточная функция управляющего устройства;  - передаточная функция объекта по управляющему воздействию;
- передаточная функция объекта по управляющему воздействию;  - передаточная функция объекта по возмущающему воздействию.
- передаточная функция объекта по возмущающему воздействию.
В соответствии со структурной схемой на рис. 5.6 уравнения движения замкнутой САУ имеют вид:
а) уравнение управляемого объекта:
 (5.8)
(5.8)
б) уравнение управляющего устройства:
 (5.9)
(5.9)
в) уравнение чувствительного элемента:
 (5.10)
(5.10)
Подставив выражение (5.9) в (5.8), получим уравнение:
 (5.11)
(5.11)
где  - передаточная функция так называемой разомкнутой системы.
- передаточная функция так называемой разомкнутой системы.
Передаточную функцию разомкнутой системы можно определить как отношение изображений управляемой величины и ошибки при нулевых начальных условиях и возмущающих воздействиях, равных нулю:
 (5.12)
(5.12)
Передаточная функция разомкнутой системы имеет весьма большое значение в теории автоматического управления, так как многие методы анализа и синтеза основаны на использовании именно этой функции.
Рассмотрим замкнутую систему, используя уравнение чувствительного элемента (5.10), которое называют уравнением замыкания. Вначале подставим выражение для ошибки управления (5.10) в уравнение (5.11):
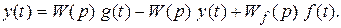 (5.13)
(5.13)
Решим (5.13) относительно управляемой величины.
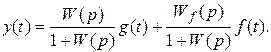 (5.14)
(5.14)
Выражение  (5.15)
(5.15)
называют передаточной функцией замкнутой системы. Она устанавливает связь между управляемой величиной и задающим воздействием при равенстве нулю возмущающих воздействий. Теперь выполним подстановку уравнения (5.11) в выражение для ошибки управления (5.10), получив тем самым уравнение, определяющее влияние воздействий g(t) и f(t) на ошибку управления:

Выражение 
называют передаточной функцией замкнутой системы по ошибке. Оно дает связь между ошибкой и задающим воздействием в замкнутой системе при равенстве нулю возмущающих воздействий.
Передаточные функции управляющего устройства  и объекта управления
и объекта управления  в общем случае есть отношения полиномов:
в общем случае есть отношения полиномов:


 (5.16)
(5.16)
Запишем с учетом обозначений (5.16) выражения для передаточных функций разомкнутой и замкнутой систем:

 (5.17)
(5.17)
Из формул (5.17) видно, что характеристический полином замкнутой системы D(p) равен сумме полиномов числителя и знаменателя разомкнутой системы.
Приравнивание нулю характеристического полинома D(p) дает характеристическое уравнение замкнутой системы: 
Оно может быть записано в более удобной форме, которая непосредственно получается из (5.15): 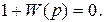
Дата добавления: 2014-11-13; просмотров: 575; Мы поможем в написании вашей работы!; Нарушение авторских прав |