Управляемость и наблюдаемость

Постановка задачи

Дана линейная многомерная стационарная система управления, поведение которой описывается уравнениями состояния и выхода:

(6.19)

где - n – мерный вектор состояния;

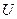- r – мерный вектор управления;

- время, - промежуток времени функционирования системы;

- мерный вектор выхода;

- матрицы размера соответственно;

- начальное состояние.

Система (6.19) называется полностью управляемой, если существует такое управляющее воздействие определенное на конечном интервале времени которое переводит систему из любого начального состояния в любое заданное конечное состояние .

Система (6.19) называется полностью наблюдаемой, если по реакции на выходе системы на промежутке времени при заданном управляющем воздействии можно определить начальное состояние .

Постановка задачи формулируется следующим образом.

Пусть известны матрицы системы (6.19). Требуется определить, является ли система полностью управляемой и наблюдаемой.

Критерии управляемости и наблюдаемости.

Условия управляемости для системы, описываемой уравнениями (6.19), определяются следующим критерием, полученным Калманом.

Необходимое и достаточное условие для управляемости системы (6.19) заключается в том, чтобы матрица

(6.20)

имела ранг, т.е. число линейно независимых строк, равный размерности вектора состояния:

Необходимые и достаточные условия для полной наблюдаемости состоят в том, чтобы матрица

(6.21)

имела ранг, равный размерности вектора состояния:

Замечание: если линейная стационарная система управления описывается уравнениями

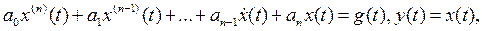
то, вводя обозначения дифференциальные уравнения системы можно записать в эквивалентной форме:

Пример определения управляемости и наблюдаемости системы

Исследовать управляемость и наблюдаемость системы:

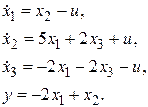
1. В уравнениях состояния и выхода выделим матрицы A, B, C:

2. Составляем матрицы управляемости и наблюдаемости:

3. Определяем ранги матриц путем приведения их к треугольной форме методом Гаусса:

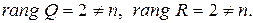
Вывод: система не является полностью управляемой и наблюдаемой.

Понятия управляемости и наблюдаемости важны, например, тогда, когда алгоритм управления формируется не в зависимости от ошибки системы, а в функции переменных состояния: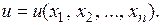

Однако, в изложенном выше смысле они не всегда совпадают с практическими представлениями. Даже если какая-либо переменная состояния и может быть вычислена по доступным для измерения выходным величинам, обработка этих величин, особенно при наличии помех, может быть сложной. Поэтому практически наблюдаемыми переменными обычно считаются те из них, которые могут быть непосредственно измерены теми или иными датчиками.