Приближенный способ построения логарифмических частотных характеристик одноконтурных систем

Структурную схему САУ можно привести к одноконтурной схеме (рис. 5.7). Если разомкнуть цепь обратной связи, получим разомкнутую систему с передаточной функцией Передаточная функция разомкнутой одноконтурной системы в общем случае может иметь вид

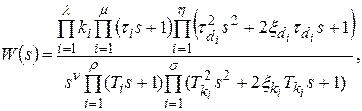(5.18)

где 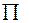- знак произведения. Обозначим .

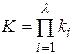Формулу (5.18) преобразуем к виду

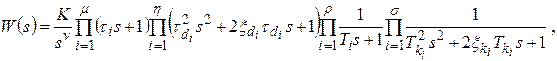
который можно записать как произведение передаточных функций типовых звеньев:

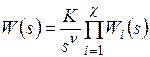, (5.19)

где общее число типовых звеньев за исключением интегрирующих (или идеальных дифференцирующих при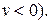

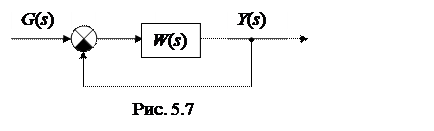Подставим в (5.19) 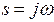и получим частотную передаточную функцию разомкнутой системы:

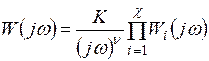. (5.20)

Все сомножители уравнения (5.20) можно записать в показательной форме:

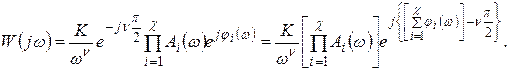(5.21)

Так как функцию можно представить в виде 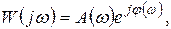то можно записать:

(5.22)

Переходя к логарифмической амплитудной частотной характеристике разомкнутой системы, получим выражение

(5.23)

из которого следует, что ЛАХ разомкнутой системы равна сумме ЛАХ типовых звеньев, последовательно соединённая цепь которых образует передаточную функцию разомкнутой системы. Первое слагаемое в правой части выражения (5.23), заключенное в скобки, есть низкочастотная ветвь ЛАХ разомкнутой системы.

Порядок построения ЛАХ одноконтурной системы по выражению (5.23):

1. Определяют сопрягающие частоты асимптотических ЛАХ отдельных звеньев САУ и отмечают их вдоль оси частот. При этом определяется интервал по оси частот для построения ЛАХ. Он находится между наименьшей сопрягающей частотой 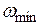и наибольшей сопрягающей частотой .

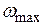2. Проводят низкочастотную асимптоту ЛАХ, которая при 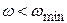определяется уравнением

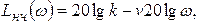(5.24)

где 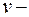порядок астатизма системы, равный количеству интегрирующих звеньев.

График уравнения (5.24) есть прямая линия с наклоном 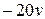дБ/дек, имеющая при частоте 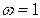ординату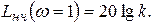

3. После каждой из сопрягающих частот 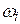наклон характеристики 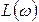изменяют по сравнению с тем наклоном, который эта характеристика имела до сопрягающей частоты 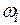, в зависимости от того, какому звену принадлежит эта частота (табл. 5.2).

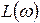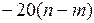4. Уточняют вид при помощи таблиц поправок. Следует отметить, что высокочастотная асимптота ЛАХ, т.е. ее часть при должна иметь наклон дБ/дек, где 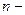порядок знаменателя, а порядок числителя передаточной функции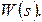

Таблица 5.2.

№ п/п	Тип звена	Передаточная функция звена	Приращение наклона асимптоты ЛАХ (дБ/дек)
	Апериодическое		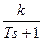-20
	Колебательное		-40
	Дифф. 1го пор.		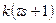+20
	Дифф. 2го пор.		+40

Логарифмическая фазово-частотная характеристика (ЛФХ) одноконтурной системы так же, как и ЛАХ, может быть получена в результате простого сложения ординат фазовых характеристик типовых звеньев, входящих в ее состав. Следует отметить, что ЛФХ при частоте, стремящейся к бесконечности, стремится к значению 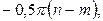где n -порядок знаменателя, а m - порядок числителя передаточной функции

ЛАХ разомкнутой системы может быть разбита на три характерных участка (рис. 5.8):

1-й участок: область низких частот – участок ЛАХ, лежащий в области частот, меньших первой сопрягающей частоты. Вид ЛАХ в этой области определяет порядок астатизма и статическую точность системы.

Для статических систем ЛАХ на этом участке – горизонтальная прямая, отстоящая от оси частот на величину 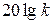. Для астатических систем n-го порядка характеристика имеет наклон, равный 2-й участок: область средних частот. Вид ЛАХ в этой области определяет в основном запас устойчивости и качество САУ. В этом интервале находится частота среза системы 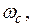характеризующая время переходного процесса при достаточных запасах устойчивости. Область средних частот заканчивается частотой 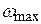, равной наибольшей сопрягающей частоте.