
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема 6. Метод переменных состояния. Управляемость и наблюдаемость непрерывных САУ
6.1. Метод переменных состояния
Метод переменных состояния основан на понятии «состояние системы». Состояние динамической системы описывается совокупностью физических переменных 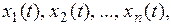 характеризующих поведение системы в будущем при условии, если известно состояние в исходный момент времени и приложенные к системе воздействия.
характеризующих поведение системы в будущем при условии, если известно состояние в исходный момент времени и приложенные к системе воздействия.
Поясним понятие переменных состояния на примере дистанционной следящей системы (рис. 6.1). Будем считать, что все звенья системы линейны. Таким образом, в рассматриваемой системе отпадает необходимость линеаризации. Разобьем систему на динамические звенья и найдем их уравнения.
Чувствительный элемент. В качестве чувствительного элемента использованы два сельсина: сельсин-датчик СД и сельсин-приемник СП, включенные по трансформаторной схеме. Ротор СД связан с командной 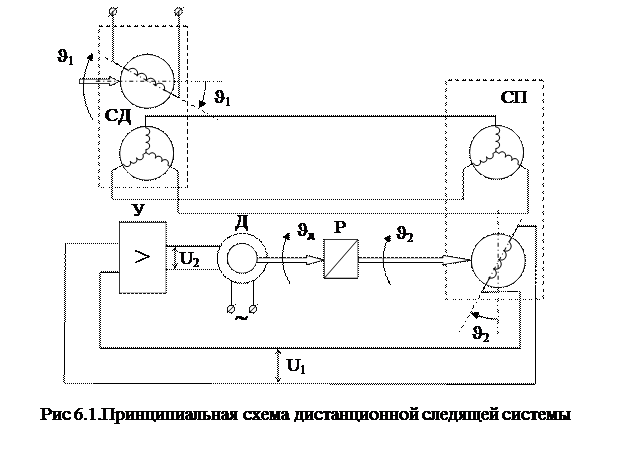 осью и поворачивается вместе с ней на угол
осью и поворачивается вместе с ней на угол 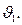 Ротор СП связан с исполнительной осью и поворачивается вместе с ней на угол
Ротор СП связан с исполнительной осью и поворачивается вместе с ней на угол 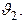 Роторная обмотка СД подключена к источнику переменного тока. Магнитный поток, создаваемый этой обмоткой, наводит э.д.с. в статорных обмотках СД, соединенных по схеме «звезда». Статорные обмотки СП служат электрической нагрузкой для СД и создают в СП магнитный поток, направление которого совпадает с магнитным потоком, создаваемым в СД. Если магнитная ось роторной обмотки СП перпендикулярна вектору индукции магнитного поля, то э.д.с. в этой обмотке не образуется и напряжение на ее выходе
Роторная обмотка СД подключена к источнику переменного тока. Магнитный поток, создаваемый этой обмоткой, наводит э.д.с. в статорных обмотках СД, соединенных по схеме «звезда». Статорные обмотки СП служат электрической нагрузкой для СД и создают в СП магнитный поток, направление которого совпадает с магнитным потоком, создаваемым в СД. Если магнитная ось роторной обмотки СП перпендикулярна вектору индукции магнитного поля, то э.д.с. в этой обмотке не образуется и напряжение на ее выходе 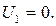 В этом случае магнитные оси роторов СД и СП взаимно перпендикулярны. При повороте командной оси перпендикулярность между осями роторов СД и СП нарушается на величину ошибки рассогласования
В этом случае магнитные оси роторов СД и СП взаимно перпендикулярны. При повороте командной оси перпендикулярность между осями роторов СД и СП нарушается на величину ошибки рассогласования
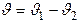 , (6.1)
, (6.1)
и на выходе роторной обмотки СП появится напряжение
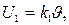 (6.2)
(6.2)
где k1-коэффициент передачи сельсинов.
Передаточная функция сельсинов равна коэффициенту передачи схемы:
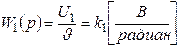 . (6.3)
. (6.3)
Усилитель. Напряжение U1 поступает на вход усилителя У. Считая усилитель инерционным звеном с очень малой постоянной времени 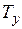 , можно записать его передаточную функцию в виде
, можно записать его передаточную функцию в виде
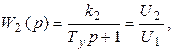 (6.4)
(6.4)
где  - коэффициент усиления по напряжению;
- коэффициент усиления по напряжению; 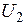 - напряжение на выходе усилителя.
- напряжение на выходе усилителя.
Дифференциальное уравнение усилителя в соответствии с его передаточной функцией имеет вид
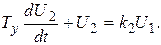 (6.5)
(6.5)
Двигатель. С выхода усилителя напряжение U2 поступает на управляющую обмотку асинхронного двухфазного двигателя Д. В установившемся режиме работы при постоянных значениях напряжения U2 и момента сопротивления Мс угловая скорость вращения выходного вала двигателя равна
wд=k3U2-k4Mc , (6.6)
где k3, k4– передаточные коэффициенты, зависящие от конструктивных параметров двигателя.
В переходных режимах, вызванных изменением величин U2 и Мс, процесс изменения скорости wд во времени может быть смоделирован дифференциальным уравнением первого порядка:
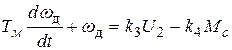 , (6.7)
, (6.7)
где Тм – электромеханическая постоянная времени двигателя.
Угол поворота выходного вала двигателя Jд связан с угловой скоростью wд кинематическим дифференциальным уравнением
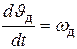 . (6.8)
. (6.8)
Уравнения (6.7) и (6.8) запишем в символической форме
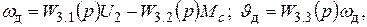 (6.9)
(6.9)
где передаточные функции 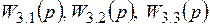 имеют вид:
имеют вид:
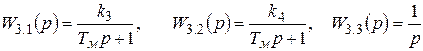 . (6.10)
. (6.10)
Редуктор. Двигатель через редуктор Р поворачивает исполнительную ось и связанный с ней ротор СП на угол 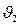 , уменьшая ошибку
, уменьшая ошибку 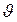 . Передаточная функция редуктора равна его коэффициенту передачи, определяемому передаточным отношением.
. Передаточная функция редуктора равна его коэффициенту передачи, определяемому передаточным отношением.
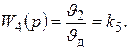 (6.11)
(6.11)
Уравнение редуктора J2=k5 Jд . (6.12)
Объединим уравнения (6.1), (6.2), (6.5), (6.7), (6.8), (6.12) в одну систему, исключив из неё алгебраические уравнения путём подстановки.

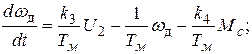 (6.13)
(6.13)
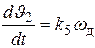 . (6.13)
. (6.13)
В качестве переменных состояния введем переменные

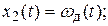
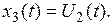
Задающее воздействие обозначим переменной 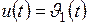 , возмущающее воздействие обозначим переменной
, возмущающее воздействие обозначим переменной 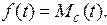
Подставляя введенные обозначения в уравнения (6.13), получим
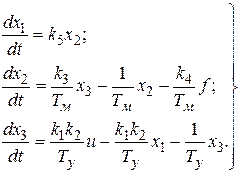 (6.14)
(6.14)
Система дифференциальных уравнений (6.14) и является системой уравнений в переменных состояния для рассматриваемой системы.
В векторно-матричной форме уравнения (6.14) имеют вид:
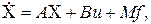 (6.15)
(6.15)
где 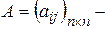 матрица размером
матрица размером 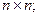
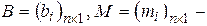 матрицы-столбцы. Порядок системы уравнений в рассматриваемом примере
матрицы-столбцы. Порядок системы уравнений в рассматриваемом примере 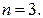
Матрицу – столбец  называют вектором состояния. Матрицы А, В, М для рассматриваемого примера имеют вид:
называют вектором состояния. Матрицы А, В, М для рассматриваемого примера имеют вид:
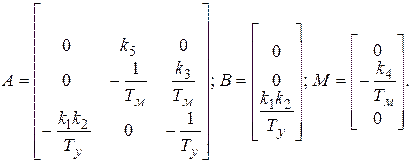 (6.16)
(6.16)
Для полного описания системы к уравнениям (6.16) необходимо добавить уравнение, устанавливающее связь между переменными состояния и выходными переменными системы регулирования. В рассматриваемом случае выходная переменная одна, это угол поворота исполнительной оси 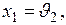 которую обозначим переменной y:
которую обозначим переменной y:
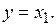 (6.17)
(6.17)
В матричной форме уравнение выхода (6.17) имеет вид:
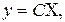 (6.18)
(6.18)
где 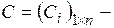 матрица выхода, в данном примере - матрица – строка размером
матрица выхода, в данном примере - матрица – строка размером 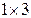 :
: 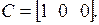
Дата добавления: 2014-11-13; просмотров: 348; Мы поможем в написании вашей работы!; Нарушение авторских прав |