Критерий устойчивости Гурвица. Этот критерий был сформулирован в 1895 году математиком А

Этот критерий был сформулирован в 1895 году математиком А. Гурвицем.

Для характеристического уравнения (7.16) составим квадратную матрицу коэффициентов, содержащую n строк и n столбцов:

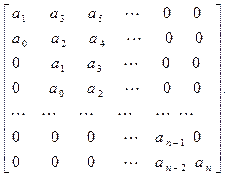(7.22)

Эта матрица составляется следующим образом.

По диагонали от левого верхнего до правого нижнего углов записывают все коэффициенты по порядку от до . Каждая строка дополняется коэффициентами с нарастающими индексами слева направо так, чтобы чередовались строки с нечетными и четными индексами. В случае отсутствия коэффициента, а также, если индекс его должен быть меньше нуля или больше n, на соответствующем месте в матрице (7.22) пишут нуль.

Критерий устойчивости сводится к тому, что при должны быть больше нуля все n определителей Гурвица, получаемых из квадратной матрицы коэффициентов. Обозначим определители Гурвица символами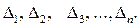

Индексы определителей Гурвица указывают их порядок, а также индекс диагонального коэффициента матрицы (7.22), который занимает место в правом нижнем углу соответствующего определителя Гурвица.

Условия устойчивости по критерию Гурвица записываются в виде:

; ….;

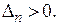
Последний определитель включает в себя всю матрицу. Но так как в последнем столбце матрицы все элементы, кроме нижнего, равны нулю, то последнее неравенство запишем в виде:

Так как предыдущее неравенство имеет вид то условие положительности определителя 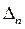, сводится к условию

Таким образом, критерий Гурвица формулируется следующим образом: для того, чтобы система была устойчива, необходимо и достаточно, чтобы при определители Гурвица были положительными.

Необходимые, но недостаточные, условия устойчивости заключаются в том, что в случае уравнения n-го порядка все коэффициенты 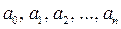должны быть положительны и ни один из них не должен равняться нулю.