Определение устойчивости по логарифмическим частотным характеристикам

Если устойчива разомкнутая система, то для устойчивости соответствующей замкнутой системы нужно, чтобы АФХ разомкнутой системы либо не пересекала действительную ось слева от точки 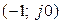(рис. 7.7 а), либо пересекала ее четное число раз, не охватывая указанную точку (рис. 7.8 а).

При использовании логарифмических частотных характеристик разомкнутой системы следует учитывать, что точке АФХ с координатами 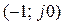соответствуют критические значения 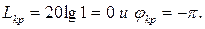В случае, когда разомкнутая одноконтурная система устойчива, замкнутая система также будет устойчива, если ЛАХ разомкнутой системы пересекает ось абсцисс при меньшей частоте, чем ЛФХ пересекает линию на уровне -p. При этом ЛФХ может либо не иметь других точек пересечения уровня -p левее частоты среза (рис. 7.7 б), либо иметь их четное количество (рис. 7.8 б).