
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задающее воздействие принимается изменяющимся по закону
 .
.
В линеаризованной системе при гармоническом задающем воздействии ошибка в установившемся режиме будет также меняться по гармоническому закону с частотой  :
: 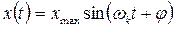 .
.
Точность системы в этом режиме может быть оценена по амплитуде ошибки
 , (8.10)
, (8.10)
где  - значение амплитудно–частотной характеристики
- значение амплитудно–частотной характеристики  при
при  .
.

Так как предполагается, что амплитуда ошибки значительно меньше амплитуды входного воздействия  , то, следовательно,
, то, следовательно,

Это позволяет с большой точностью выражение (8.10) заменить приближенным
 , (8.11)
, (8.11)
где  - значение АФЧХ разомкнутой системы при
- значение АФЧХ разомкнутой системы при 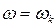 .
.
Формула (8.11) широко используется при расчете системы методом ЛАХ. Простота выражения (8.11) позволяет легко сформулировать требования к ЛАХ, которые необходимо выполнить, чтобы амплитуда ошибки в установившемся режиме при  была не больше заданного значения
была не больше заданного значения  . Требуемое значение модуля частотной передаточной функции разомкнутой системы в децибелах
. Требуемое значение модуля частотной передаточной функции разомкнутой системы в децибелах  .
.
 Это значение модуля необходимо отложить на логарифмической сетке при частоте управляющего воздействия
Это значение модуля необходимо отложить на логарифмической сетке при частоте управляющего воздействия  Полученная точка Ak (рис. 8.2) обычно называется контрольной точкой, ниже которой ЛАХ не должна проходить.
Полученная точка Ak (рис. 8.2) обычно называется контрольной точкой, ниже которой ЛАХ не должна проходить.
Дата добавления: 2014-11-13; просмотров: 356; Мы поможем в написании вашей работы!; Нарушение авторских прав |