Критерий устойчивости Найквиста

Данный критерий вытекает из принципа аргумента. Характерной его особенностью является то, что вывод об устойчивости или неустойчивости замкнутой системы делается в зависимости от вида АФЧХ или ЛЧХ разомкнутой системы.

Передаточную функцию разомкнутой системы можно представить в виде (см. (5.17)):

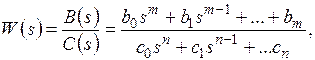где m<n.

Введем в рассмотрение вспомогательную функцию

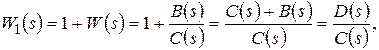(7.25)

где характеристический полином замкнутой системы, степень которого совпадает со степенью характеристического полинома разомкнутой системы :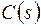

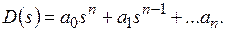
Для первого и последнего коэффициентов полинома справедливы равенства: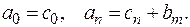

Сделаем подстановку 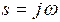в выражение (7.25):

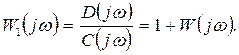(7.26)

Предположим, что разомкнутая система устойчива. Это значит, что все корни характеристического уравнения =0 находятся в левой части КП и изменение аргумента вектора при возрастании w от 0 до 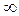будет

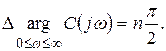
Изменение аргумента вектора 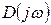при возрастании w от 0 до в общем случае равно (см. (7.24)) 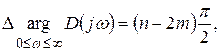где m-число корней характеристического уравнения 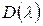=0, лежащих в правой части КП.

Частотную характеристику 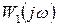(7.26) запишем в показательной форме:

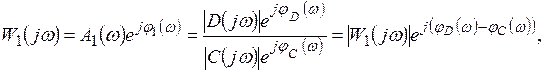(7.27)

где амплитудная частотная характеристика функции ; .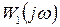

Изменение аргумента вектора при возрастании частоты w от 0 до равно разности изменений аргументов 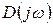и :

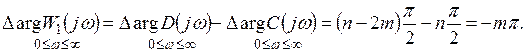
Замкнутая система будет устойчивой, если m=0, т.е. если

(7.28)

Для построения АФХ определим начальное ( ) и конечное ( ) положения вектора на КП. С этой целью вычислим модуль вектора 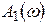и аргумент 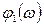на границах частотного интервала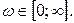

Из выражения (7.27) получим граничные значения :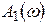

1)

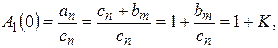
где К- коэффициент усиления разомкнутой системы;

2) 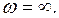В этом случае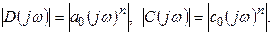

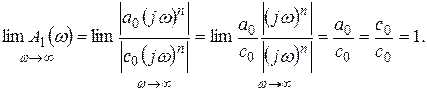
Значения аргументов векторов 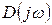и при равны при любом расположении корней уравнени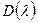й =0 и 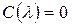на КП. Для конечного значения аргумента вектора 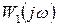получим:

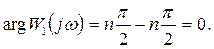
Таким образом, направление вектора 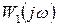при совпадает с положительным направлением вещественной оси комплексной плоскости, а модуль вектора 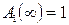(рис. 7.3 а).

Начальное значение аргумента вектора 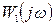определим из выражения (7.28):

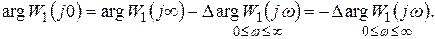(7.29)

Для системы, устойчивой в замкнутом состоянии, 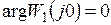. Следовательно, направление вектора при 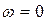также совпадает с положительным направлением вещественной оси КП, а модуль вектора 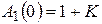(рис. 7.3 а).

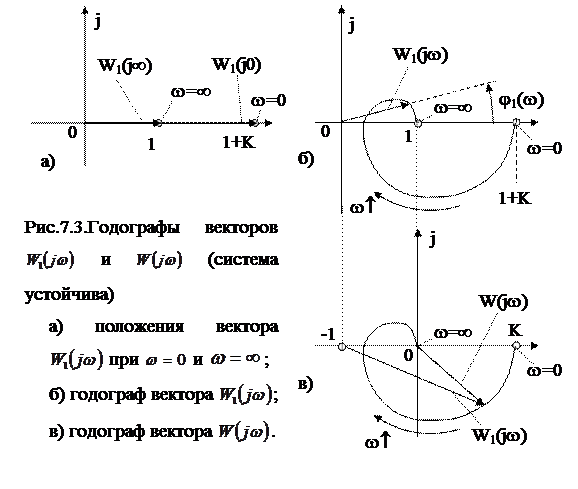
Условие устойчивости замкнутой системы (7.28) будет выполнено лишь в том случае, если при возрастании w от 0 до ¥ годограф вектора не охватит начало координат (рис. 7.3 б).

От годографа вектора можно перейти к АФХ разомкнутой системы 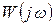в соответствии с выражением (7.26):

(7.30)

Единицу в формуле (7.30) можно рассматривать как вектор – орт оси вещественных чисел. Если сместить кривую 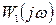влево на единицу, получим АФХ разомкнутой системы (рис. 7.3 в).

Амплитудно–фазовый критерий устойчивости можно сформулировать следующим образом:

Если разомкнутая система устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно – фазовая характеристика разомкнутой системы не охватывала точку с координатами (-1; j 0).

Если замкнутая система неустойчива, то уравнение 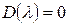содержит корни с положительными вещественными частями (m¹0). Результирующий угол поворота вектора 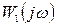при возрастании частоты от 0 до 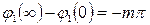. Это означает, что для неустойчивой замкнутой системы годограф вектора 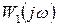охватывает начало координат на угол mp по часовой стрелке.

Пример .Дана передаточная функция разомкнутой системы

.

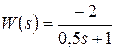Разомкнутая система устойчива, так как характеристическое уравнение 0,5l+1=0 имеет отрицательный вещественный корень .

Построим вспомогательную функцию :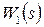

.

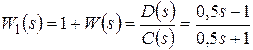Замкнутая система неустойчива, так как характеристическое уравнение имеет положительный вещественный корень .

Сделаем подстановку 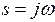в выражение для :

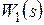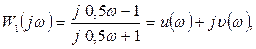
где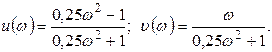

Начальное положение вектора при :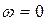

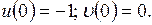
Конечное положение вектора при :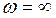

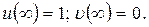
Так как при любых значениях частоты 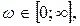годограф вектора находится в верхней части КП (рис. 7.4). Нетрудно убедиться, что пр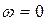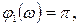и при 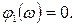При возрастании w от 0 до вектор 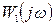повернется на угол т.е. по часовой стрелке.

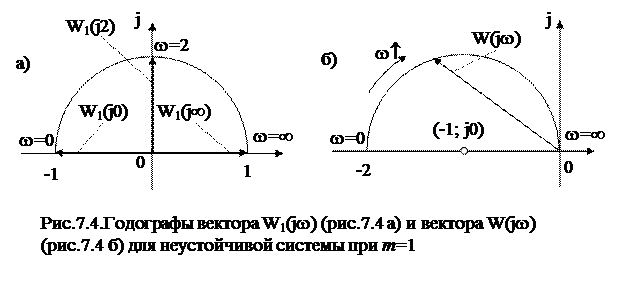
Перейдя от 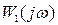АФХ к АФХ 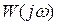по формуле (7.30) 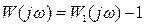, получим годограф вектора 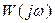, охватывающий точку с координатами 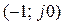(рис. 7.4 б).

Снимем теперь ограничения на корни характеристического полинома разомкнутой системы 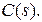Будем полагать, что в нем кроме корней с отрицательными вещественными частями есть нулевые корни.

При наличии одного нулевого корня знаменатель функции 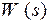будет иметь выражение

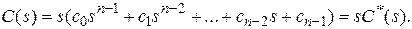
Запишем частотную функцию разомкнутой системы

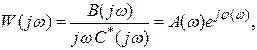(7.31)

где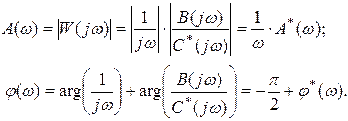

При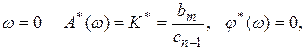

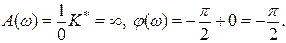
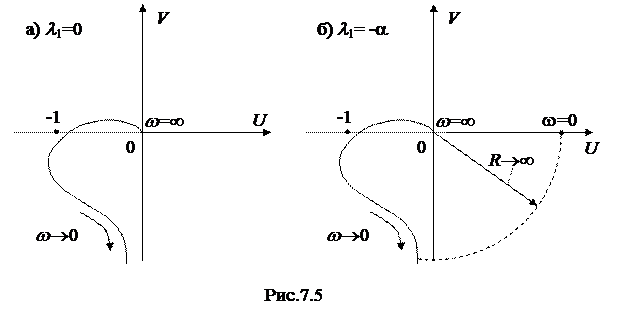В результате на частоте w = 0 АФХ разомкнутой системы будет иметь разрыв непрерывности (рис. 7.5а). Для получения определенности в ходе АФХ заменим нулевой корень бесконечно малым вещественным отрицательным корнем 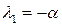. Тогда полином 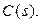примет вид а в знаменателе частотной функции 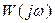вместо 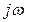получим сомножитель модуль которого при w=0 есть бесконечно малая величина, а фаза изменяется от нуля при w=0 до p/2 при 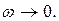При этом модуль функции (7.31) А(0) будет стремиться к бесконечности, а фаза будет изменяться от нуля до ‑p/2.

Таким образом, АФХ разомкнутой системы дополнится по часовой стрелке четвертью окружности с радиусом , начало которой находится на вещественной оси, и разрыв непрерывности будет устранен (рис. 7.5 б). Кроме того, так как нулевой корень заменен вещественным отрицательным корнем, то разомкнутую систему можно считать устойчивой. Все это означает, что для исследования устойчивости замкнутой системы можно применять приведенную ранее формулировку критерия Найквиста.