Интегрирующее звено

У интегрирующего звена скорость изменения выходной величины пропорциональна входной величине:

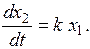(4.16)

Уравнение (4.16) получим из (4.1) при . При этом передаточный коэффициент

Умножим (4.16) на dt и проинтегрируем по времени от нуля до текущего значения t.

(4.17)

Решение уравнения (4.17):

(4.18)

Согласно (4.18) выходная величина пропорциональна интегралу от входной величины, откуда и название звена.

Применив к уравнению (4.16) преобразование Лапласа при нулевых начальных условиях, получим:

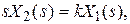
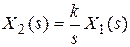(4.19)

Из (4.19) следует, что интегрирующее звено имеет передаточную функцию (4.20)

С помощью интегрирующего звена можно моделировать, например, кинематическую связь между углом a и угловой скоростью w поворота некоторого механического элемента:

Характеристики звена:

а)Переходная функция звена определяется выражением

(4.21)

График функции (4.21) есть прямая, проведённая из начала координат под углом

б) Весовая функция интегрирующего звена

(4.22)

есть ступенчатая функция.

в) Частотная передаточная функция

(4.23)

где

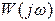При изменении w от 0 до (рис.4.5) конец вектора движется по отрицательной части мнимой оси от до 0. Интегрирующее звено создает отставание выходной величины от входной на 90^° при всех частотах. Амплитуда выходной величины уменьшается с возрастанием частоты.

г) ЛАХ интегрирующего звена определяется формулой

(4.24)

Выражение (4.24) есть уравнение прямой с наклоном -20 дБ/дек, проходящей при частоте 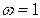через точку Пересечение графиком функции (4.24) оси частот происходит при w=k.