Уравнение неразрывности для струйки.

Первое свойство струйки, говорящее о том, что боковая поверхность непроницаема для частиц, по существу выражает закон сохранения секундной массы. Действительно, если через сечение 1-1 в единицу времени вошла масса 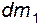, то за то же время через сечение 2-2 должна выйти масса , равная 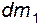. Массу жидкости, протекающую через поперечное сечение струйки в единицу времени называют элементарным массовым расходом и обозначают .

Легко убедиться в том, что , где dA - площадь поперечного сечения струйки. Действительно, выражая параметры, входящие в это соотношение через единицы физических величин, получаем

.

Из сказанного выше следует, что

(4.10)

Это и есть уравнение неразрывности для струйки. Если жидкость несжимаема, т.е. 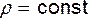, то и

(4.11)

При этом произведение udA выражает элементарный объемный расход - dQ.