Угловые деформации.

Из рис. 4.5 следует, что угловая деформация (скашивание) может возникнуть из-за разности скоростей, перпендикулярных ребрам (частично этот вопрос уже обсуждался в разделе 2.2). Для упрощения целесообразно ограничиться лишь одной гранью, показанной на рис. 4.6.

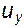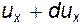Пусть компоненты скорости в точке A равны , , . Найдем скорости в точке B, считая, что движение установившееся и, следовательно, все производные по t равны нулю. Приращение компоненты скорости при переходе из одной точки пространства в другую можно представить как u+du. Так для проекции можем записать , где

(4.13)

Аналогичные выражения можно записать и для других проекций.

Рассмотрим приращение при переходе от точки A к точке B. В этом случае 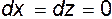, т.е.

Предположим, что за время dt за счет разности скоростей в точках A и B ребро займет положение AB'.

Аналогично рассуждая относительно скорости 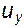в точках A и D получим:

Точка A: 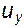(по условию)

Точка D: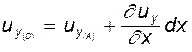

За счет разности этих скоростей точка D займет позицию D'. Таким образом

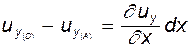
Путь, проходимый точкой B за время dt в положение B', определяет величину скашивания, которую можно найти как

Угловая деформация характеризуется тангенсом угла . При этом

(имея в виду, что ).

Вследствие малости угла можно считать, что .

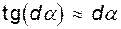Аналогично,

Полное скашивание первоначально прямого угла A определяется как сумма

(4.14)

Здесь следует обратить внимание на одно весьма существенное обстоятельство: рассматриваемое перемещение ребер вызвано не только деформацией, но и вращением частицы. Действительно, если бы грань только деформировалась без вращения, то ребра повернулись бы на одинаковый угол навстречу друг другу. Наоборот, если бы происходило только вращение, то ребра поворачивались бы на одинаковый угол в направлении вращения. Следовательно, в общем случае движение элемента можно рассматривать как сумму деформационного и вращательного движений, и таким образом определить и . 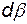Рассмотрим деформацию прямого угла A, считая, что вращение происходит против часовой стрелки. Чисто деформационное движение будем характеризовать углами 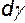, а чисто вращательное - .

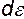Из рис. 4.7 следует, что

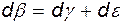
либо ,

откуда

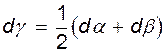(4.15)

Вычитая, получим

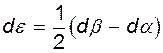(4.16)

Таким образом, деформация характеризуется полусуммой углов, а вращение - полуразностью. Имея в виду (4.14), можем записать:

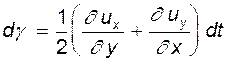(4.17)

Скорость угловой деформации, происходящей вокруг оси z

(4.18)

И по аналогии

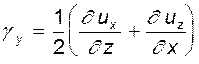(4.19)

(4.20)

Выражение есть угловая скорость вращения жидкой частицы. Проекции угловых скоростей

(4.21)

(4.22)

(4.23)

Соотношения (4.21­4.23) играют исключительно важную роль в механике жидкости. Они устанавливают связь между угловой и поступательной скоростями жидкой частицы. Вопрос о знаках чисто условный. В гидромеханике поворот против часовой стрелки считается положительным, по часовой - отрицательным.

В векторной форме выражение для угловой скорости может быть записано как

(4.24)

Заменяя 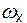, и их выражениями по (4.21-4.23) получаем:

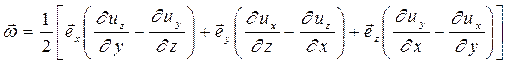(4.25)

Сопоставляя выражение в квадратных скобках с формулой (1.8) видим их полную идентичность, поэтому можем записать:

(4.26)

либо

(4.27)

Формула (4.27) раскрывает гидромеханический смысл вихря (рото­ра) векторного поля. Если 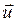характеризует поле мгновенных скоростей, то векторное поле 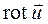представляет собой поле удвоенных угловых скоростей частиц жидкости этого поля.