Теорема Стокса.

В движущейся жидкости рассматриваем вихревое поле и выделяем в нем малый замкнутый контур со сторонами dx и dy (рис. 5.5). Пусть в начале координат скорости будут и 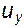. Запишем выражение для элементарной циркуляции по этому контуру, имея в виду, что поток двумерный: .

Рассмотрим контур OABC. Если вдоль OA скорость , то вдоль CB ее приращение составит , и аналогично вдоль AB - . Это следует из выражения для полного дифференциала скорости, например, .

Запишем теперь выражение для элементарной циркуляции вдоль контура OABCO. Имеем:

Раскрывая скобки и выполнив сокращения, получаем

Из чего следует, что циркуляция по бесконечно малому замкнутому контуру равна интенсивности вихря, пронизывающего этот контур.

Этот вывод легко обобщить и на случай произвольной кривой конечных размеров (см., например, Аржаников Н.С. и Мальцев В.Н. Аэродинамика. - М.: Оборонгиз, 1956 - 483 с.; упомянутую выше книгу Н.Я.Фабриканта).

Таким образом, можем записать:

(5.14)

Это и есть формула Стокса, показывающая, что циркуляция по произвольному контуру равна сумме интенсивностей (напряжений) вихрей, пронизывающих поверхность, натянутую на контур.