Уравнение Лапласа.

Операция дивергенции над градиентом скалярной функции приводит к оператору Лапласа. Если в качестве скалярной функции использовать потенциал скорости, то можно записать

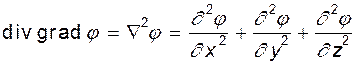(6.6)

Для несжимаемой жидкости , а (см. формулу 6.5). Таким образом

(6.7)

либо

(6.8)

Выражения (6.7) и (6.8) носят название уравнения Лапласа. Таким образом, для нахождения потенциала скорости необходимо проинтегрировать уравнение Лапласа. Любая функция, удовлетворяющая этому уравнению, носит название гармонической. Следовательно, потенциал скорости является гармонической функцией. Как любое дифференциальное уравнение, уравнение Лапласа имеет бесчисленное множество решений, поэтому для того, чтобы однозначно определить потенциал скорости, необходимо задать граничные условия. Для задач, связанных с обтеканием тел, так называемых внешних задач гидромеханики, такими условиями являются и .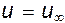

Первое условие характеризует безотрывность течения (ра­венство нулю нормальной компоненты скорости). Второе - показывает, что вдали от тела распределение скоростей известно.

Поверхности (либо линии для двумерных потоков), в каждой точке которых , называются эквипотенциальными.