Функция тока плоского течения.

В практических задачах гидромеханики двумерных потоков широчайшее применение находит понятие о функции тока. Рассмотрим двумерный поток и ограничимся несжимаемой жидкостью.

Как было показано, дифференциальное уравнение линии тока имеет вид

либо

. (6.10)

Запишем уравнение неразрывности для этого случая, которое будет иметь вид

. (6.11)

Аналогично тому, как это делалось при рассмотрении потенциала скорости, поставим вопрос об условиях необходимых и достаточных для того, чтобы выражение (6.10) являлось полным дифференциалом какой-то скалярной функции. Применим к (6.10) условия Клеро (равенство взятых накрест производных). Имеем:

и .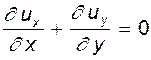

Но это есть не что иное, как уравнение неразрывности (6.11) для плоского потока, которое удовлетворяется всегда, если только движение существует. Следовательно, можно записать:

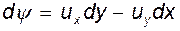(6.12)

где носит название функции тока. С другой стороны, поскольку, как показано выше, является полным дифференциалом, то можно записать:

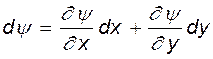(6.13)

Сопоставляя (6.12) и (6.13), получаем

; (6.14)

Из чего следует, что если функция тока течения известна, то можно определить компоненты скорости в любой точке пространства. Сопоставляя (6.10) и (6.12) приходим к выводу, что если частица движется вдоль линии тока, то функция тока остается постоянной (при 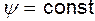, и (6.12) превращается в (6.10)). Проверим теперь, является ли функция тока гармонической функцией, т.е. удовлетворяет ли она уравнению Лапласа.

Для плоского потенциального течения 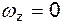, но , откуда 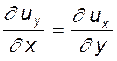. Из (6.14) и , следовательно

,

откуда

.

Таким образом, функция тока, как и потенциал скорости, является гармонической функцией. И еще одно важное обстоятельство. Если потенциал скорости существует только в потенциальном потоке, то функция тока этим условием не ограничена. Это объясняется тем, что уравнение неразрывности, которое используется для получения этого понятия, справедливо как для вихревого, так и для безвихревого движений.