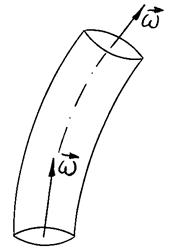
Интенсивность вихря.

Понятие интенсивности вихря достаточно абстрактно и вводится чисто математически. Напомним, что потоком векторного поля называют интеграл вида

(5.4)

Поскольку вихрь скорости (ротор) есть вектор, то вместо 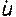можно подставить 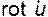, что и приводит нас к понятию интенсивности вихря, т.е. интенсивность вихря ­ это поток вектора вихря

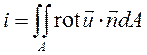(5.5)

Можно использовать и другую форму записи: ;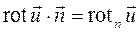

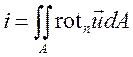(5.6)

Имея в виду, что , можем записать

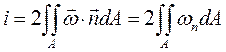(5.7)

Воспользуемся формулой Гаусса-Остроградского и перейдем от интеграла по поверхности к интегралу по объему. Имеем:

.

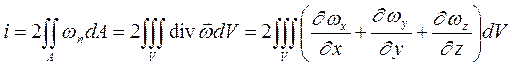Раскроем выражение, стоящее под знаком интеграла, имея в виду, что проекции вектора вихря имеют вид:

;

;

.

Имеем

.

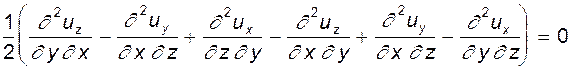Следовательно, можно записать

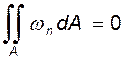(5.8)

Заметим, что это выражение по структуре напоминает уравнение неразрывности.

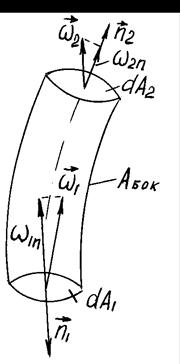
Применим (5.8) к вихревому шнуру (рис. 5.2). На боковой поверхности , так как 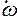направлен по касательной к поверхности. Поэтому можем записать

;

.

Если допустить, что в пределах сечения 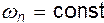, то

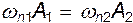(5.9)

Либо в общем случае

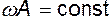(5.10)

т.е. это своеобразное «уравнение неразрывности». Полученный результат носит название теоремы Гельмгольца о вихрях, которую можно сформулировать следующим образом: интенсивность вихревого шнура на всей его протяженности остается постоянной. Из выражения (5.10) следует и другой весьма важный вывод, сделанный Г.Гельмгольцем в 1855 г. в работе «Об интегралах уравнений, соответствующих вихревым движениям».Так как произведение остается неизменным, то уменьшение площади сечения шнура должно приводить к увеличению угловой скорости вращения частиц. При 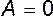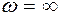, что физически невозможно. Следовательно, вихрь не может зарождаться либо оканчиваться в толще жидкости. Окончательно развившись, он должен замкнуться либо на твердую поверхность, либо сам на себя, т.е. образовать вихревое кольцо. Подробное описание этого явления можно найти в книге: Фабрикант Н.Я. Аэродинамика. - М.: Наука, 1964. - 814 с.

Понятие об интенсивности является весьма важным, но, к сожалению, непосредственное определение этой величины экспериментальным путем связано с непреодолимыми трудностями. Кроме того, если пытаться распространить это понятие на вихри конечных размеров, то по аналогии со средней скоростью пришлось бы вводить понятие о средней угловой скорости, что связано с определенными трудностями чисто математического характера. Поэтому гидромеханика избрала другой путь, заменив это понятие другим, более удобным для целей практики. К рассмотрению этого понятия, называемого циркуляцией скорости, мы и приступим.