Потенциал скорости.

Сущность теоремы Стокса, по существу, сводится к утверждению о равенстве числовых значений интенсивности вихря и циркуляции, т.е. , либо

.

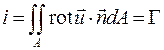С другой стороны, для потенциального потока по его определению , т.е. в потенциальном поле циркуляция по замкнутому контуру равна нулю.

Запишем выражения для проекций угловых скоростей.

Из сказанного выше следует, что для безвихревого (потенци­ального) движения 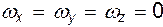. Следовательно, в этом случае

; ; (6.1)

Эти соотношения позволяют существенным образом упростить вычисления компонент скорост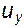и , и .

Рассмотрим выражение

(а)

Оно построено аналогично известному из механики твердого тела выражению для элементарной работы. Зададимся вопросом, в каком случае (а) является полным дифференциалом. Напомним, что если выражение для работы является полным дифференциалом, то силы называются консервативными или имеющими потенциал. Ответ на поставленный вопрос был дан Алесисом Клодом Клеро (с жизнью и деятельностью этого удивительного ученого можно познакомиться по превосходной книге: Идельсон Н.И. Этюды по истории небесной механики. - М.: Наука, 1975. - 494 с.)

Клеро показал, что выражение типа (а) является полным дифференциалом, если обеспечивается равенство накрест взятых производных. Соотношения (6.1) как раз и удовлетворяют этому требованию, т.е. взятые накрест производные в (а) дают соотношения (6.1). Таким образом, при потенциальном движении выражение (а) является полным дифференциалом какой-то функции , и

(6.2)

С другой стороны, по общему правилу полный дифференциал может быть представлен как

(6.3)

Сопоставляя (6.2) и (6.3), получаем

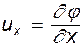; ; (6.4)

По предложению Гельмгольца функцию называют потенциалом скорости.

Таким образом, всякому движению жидкости, происходящему без вращения частиц, соответствует свой потенциал скорости. Справедливо и обратное утверждение: если существует потенциал скорости, то движение происходит без вращения частиц.

Соотношения (6.4) можно получить и другим путем. Поскольку разные подходы к одному и тому же вопросу способствуют углубленному его пониманию, то получим эти же соотношения, используя другую методику.

Как уже отмечалось, условием потенциальности является . С другой стороны, как показано при рассмотрении операций второго порядка, операция ротора над градиентом какой-то ска­лярной функции тождественно равна нулю, т.е.

Сопоставляя эти соотношения, можем записать

(6.5)

Это означает, что вектор скорости можно рассматривать как градиент какой-то скалярной функции . Раскроем значения и . Имеем

;

.

Откуда, учитывая (6.5), получаем

; ; ,

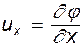т.е. вновь приходим к соотношениям (6.4).

Пока что остается открытым вопрос о необходимости и целесообразности введения понятия о потенциале скорости. Чтобы разобраться в этом, следует иметь в виду, что к числу центральных задач гидромеханики относится определение сил, действующих на тела, обтекаемые потоками жидкости либо газа. Решение этих задач непосредственно связано с необходимостью расчета поля скоростей, т.е. определением проекций скоростей ( , , ) в каждой его точке. Из выражений (6.4) непосредственно следует, что все три компоненты скорости могут быть определены, если известна лишь одна величина - потенциал скорости. Таким образом, знание потенциала скорости существенно упрощает расчет поля. Однако немедленно возникает следующая проблема - как же найти потенциал скорости течения. Чтобы решить ее, необходимо прежде всего уяснить некоторые свойства, присущие потенциалу.