
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функции для анализа обыкновенных аннуитетов
В финансовой практике часто встречаются операции, характеризующиеся возникновением потоков платежей (денежных поступлений и выплат), распределенных во времени. Потоки платежей, при которых выплаты (поступления) денежных средств осуществляются равными суммами через одинаковые интервалы времени,принято называть обыкновенным или регулярным аннуитетом.Как правило, подобные потоки платежей возникают при проведении кредитно-депозитных операций, формировании различных фондов, долгосрочной аренде и т.п.
Количественный анализ финансовых данных в Excel при проведении таких операций сводится к исчислению следующих основных характеристик:
· текущей величины (present value – PV) потока платежей;
· будущей величины (future value – FV) потока платежей;
· величины отдельного платежа (payment – P);
· нормы доходности (цены) в виде процентной ставки (interest rate – r);
· числа периодовпроведения финансовой операции (например, лет, месяцев, и т.д.).
Используемые при этом методы базируются на технике исчисления сложных процентов.
Табличный процессор Excel предоставляет широкие возможности по моделированию подобных расчетов при помощи соответствующих встроенных в Excel финансовых функций: БC(), КПЕР(), СТАВКА(), ПЛТ(), ПС().
Все функции данной группы имеют одинаковый набор базовых аргументов:
ü процентная ставка(норма доходности или цена заемных средств);
ü срок(число периодов) проведения операции;
ü величина периодического платежа;
ü начальная сумма;
ü будущая стоимость (величина) денежных средств;
ü тип начисления процентов(1- начало периода, 0 – конец периода).
Рассмотрим применение вышеперечисленных функций в проведении финансовых расчетов и анализе обыкновенных аннуитетов на конкретном примере.
Предположим, Ваша фирма решила создать специальный фонд для погашения своих долгосрочных обязательств (кредитов, займов), срок погашения которых наступит, например, через 5 лет, путем периодического (ежегодного) пополнения депозита в банке. Начальная сумма депозита составляет 10000 тыс. руб. Размер ежегодных платежей – 1000 тыс. руб. Процентная ставка по банковскому депозиту – 15%.
Необходимо определить величину фонда к концу 5-го года.
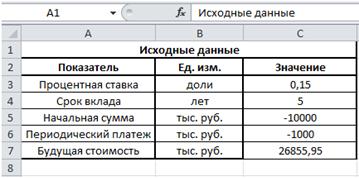
Для решения поставленной задачи выполните следующие действия:
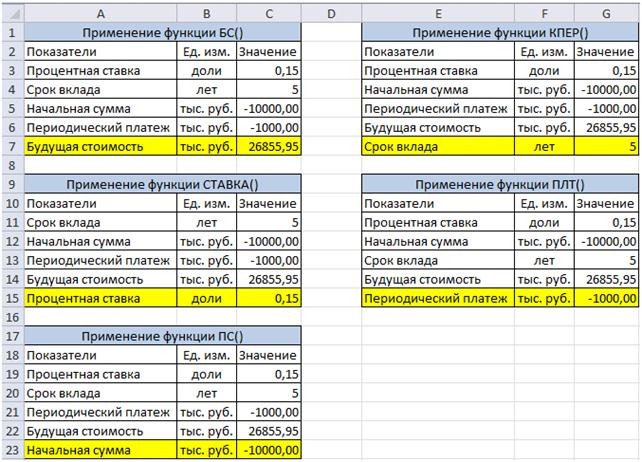
1) Введите исходные данные на рабочий лист. Диапазон таблицы С3:С6 содержит входные данные для расчета величины денежного фонда, т.е. будущей стоимости вложений (инвестиций).

2) Установите курсор в ячейку рабочего листа, где будет рассчитана будущая стоимость вложений (депозита), в данном случае в ячейку C7.
3) Выполните команду Формулы / Библиотека функций / Вставить функциюили нажмите кнопку  Строки формул. В категорииФинансовыеиз списка выберите функцию БC( ). Нажмите ОК.
Строки формул. В категорииФинансовыеиз списка выберите функцию БC( ). Нажмите ОК.
4) Excel выведет окно ввода аргументов выбранной функции. Введите в каждое поле запроса ссылку на ячейку, содержащую требуемое значение.
Функция БС( ) – позволяет определить будущую величину вклада (Future Value – FV) на основе периодических постоянных платежей при заданных величинах процентной ставки, числа периодов выплат и начальной суммы вклада.
Функция имеет следующий синтаксис:
=БС(норма; число периодов; выплата; нз; тип),
где: норма – процентная ставка (норма доходности по депозиту);
число периодов – срок (число периодов) проведения операции;
выплата – величина периодического платежа;
нз– начальная стоимость вложений (депозита);
тип – тип начисления процентов, является необязательным аргументом.
(0 – в конце периода; 1 – в начале периода). По умолчанию начисление процентов осуществляется в конце периода.
Следует обратить внимание на особенности задания аргументов:
Если процентная ставка задается как абсолютная величина, она должна иметь вид десятичной дроби, например как в примере: 15% – 0,15. Периодический платеж и начальная сумма задаются со знаком минус, т.к. в данной операции для фирмы они означают выплаты (расходование) денежных средств. Такие правила применимы для всех финансовых функций. В зависимости от условия поставленной задачи, значения периодического платежа и начальной стоимости могут быть введены в функцию как в виде положительных, так и отрицательных величин. Это зависит от того, какой экономический субъект проводит подобные расчеты. Кроме того, можно на этапе ввода аргументов определить конечный результат, возвращаемый функцией, который отображается внизу диалогового окна ввода аргументов.
MS Excel при расчетах характеристик денежных аннуитетов выражает каждый показатель исходя из следующего соотношения:
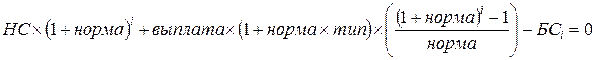 ,
,
где: НC – начальная (текущая) стоимость вклада;
БСi – будущая стоимость вклада через число периодов i ;
норма – процентная ставка (норма доходности);
выплата – периодический платеж;
i – порядковый номер периода поведения финансовой операции;
тип – тип начисления процентов.
Таким образом, будущая стоимость вложений определяется по формуле:
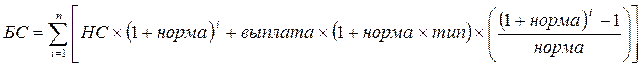 ,
,
Для нашего предприятия будущее значение банковского депозита в конце 5-го года будет следующим:
=БС(0,15;5;-1000;-10000) (Возвращаемый результат: 26855,95 тыс. руб.).
Для банка, определяющего будущую сумму возврата средств по данному депозиту, функция имела бы следующий вид:
=БС(0,15;5;1000;10000) (Возвращаемый результат: -26855,95 тыс. руб.).
Функция КПЕР( ) – позволяет определить число выплат (поступлений) денежных средств, если известны процентная ставка, периодический платеж, начальная и будущая величины потоков платежей.
Предположим, необходимо определить количество периодов платежей (в данном примере – число лет). Функция будет выглядеть следующим образом:
=КПЕР(0,15;1000;10000;26855,95)(Возвращаемый результат: 5),
где: 0,15 – процентная ставка по депозиту; 1000 – периодический платеж; 10000 – первоначальная сумма депозита; 26855,95 – будущая величина депозита.
Функция СТАВКА( ) – вычисляет процентную ставку, которая в зависимости от условий операции может выступать либо в качестве цены, либо в качестве нормы рентабельности данной операции. Имеет аргументы:
СТАВКА(кпер, плт, пс, [бс], [тип], [прогноз])
где: кпер – обязательный. Общее число периодов платежей для ежегодного платежа;
плт – обязательный. Выплата, производимая в каждый период; это значение не может меняться в течение всего периода выплат. Обычно аргумент "плт" состоит из основного платежа и платежа по процентам, но не включает других налогов и сборов. Если он опущен, аргумент "пс" является обязательным.
пс – обязательный. Приведенная (текущая) стоимость, т. е. общая сумма, которая на данный момент равноценна ряду будущих платежей;
бс – необязательный. Значение будущей стоимости, т. е. желаемого остатка средств после последней выплаты. Если аргумент "бс" опущен, предполагается, что он равен 0 (например, будущая стоимость для займа равна 0).
тип – необязательный. Число 0 или 1, обозначающее, когда должна производиться выплата (0 или опущен – в конце периода, 1 – в начале периода;
прогноз – необязательный. Предполагаемая величина ставки. Если аргумент "прогноз" опущен, предполагается, что его значение равно 10 %.
Пусть в нашем примере будет неизвестна процентная ставка по банковскому депозиту. Тогда для ее расчета воспользуемся функцией СТАВКА( ):
=СТАВКА(5;-1000;-10000;26855,95)(Возвращаемый результат: 15%).
Для корректной работы функции платеж и сумма вклада должны быть заданы в виде отрицательных величин.
Функция ПЛТ( ) – применяется в том случае, если необходимо определить величину периодического платежа по ссуде при заданных величинах будущей стоимости вложений на основе постоянных выплат, срока, процентной ставки и настоящей стоимости вложений. Имеет следующие аргументы:
ПЛТ(ставка; кпер; плт; [бс]; [тип])
Где: ставка - обязательный аргумент. Процентная ставка по ссуде;
кпер – обязательный аргумент. Общее число выплат по ссуде;
пс – обязательный аргумент. Приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей, называемая также основной суммой;
бс – необязательный аргумент. Требуемое значение будущей стоимости, т. е. желаемого остатка средств после последнего платежа. Если этот аргумент опущен, предполагается, что он равен 0 (будущая стоимость для займа равна 0);
тип – необязательный аргумент. Число 0 (нуль) или 1, обозначающее, когда должна производиться выплата.
Формула расчета периодического платежа, исходя из вышеприведенного соотношения, будет иметь следующий вид:
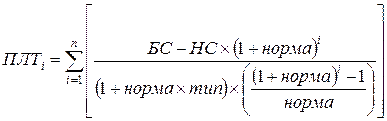 .
.
Предположим, в нашем примере необходимо определить величину периодического платежа при заданных входных параметрах. Функция будет иметь следующий вид:
=ПЛТ(0,15;5;-10000;26855,95)(Возвращаемый результат: -1000).
Полученный отрицательный результат для фирмы означает отток денежных средств. Для банка, соответственно, наоборот.
Функция ПС( ) – позволяет определить текущую(т.е. на момент начала операции – present value) стоимость аннуитета, если известны 4 обязательных параметра (процентная ставка; число периодов; начальная стоимость; будущая стоимость денежных средств). Имеет следующие аргументы:
ПС(ставка, клер, плт, [бс], [тип])
где: ставка - обязательный. Процентная ставка за период. Например, если получен кредит на автомобиль под 10 процентов годовых и выплаты производятся ежемесячно, процентная ставка за месяц составит 10%/12 (0,83%). В качестве значения аргумента "ставка" нужно ввести в формулу 10%/12, 0,83% или 0,0083.
кпер – обязательный. Общее число периодов платежей для ежегодного платежа. Например, если получен кредит на 4 года на покупку автомобиля и платежи производятся ежемесячно, то кредит имеет 4*12 (или 48) периодов. В качестве значения аргумента "кпер" в формулу нужно ввести число 48.
плт – обязательный. Выплата, производимая в каждый период и не меняющаяся на протяжении всего периода ежегодного платежа. Обычно аргумент "плт" состоит из выплат в счет основной суммы и платежей по процентам, но не включает в себя другие сборы или налоги. Например, ежемесячная выплата по кредиту в размере 10 000 р. под 12 процентов годовых на 4 года составит 263,33р. В качестве значения аргумента "плт" нужно ввести в формулу число -263,33.
бс – необязательный. Значение будущей стоимости, т.е. желаемого остатка средств после последнего платежа. Если аргумент "бс" опущен, предполагается, что он равен 0 (например, будущая стоимость для займа равна 0). Предположим, что для определенной цели требуется накопить 50 000 р. за 18 лет: в этом случае будущая стоимость равна 50 000 р. Предположив, что заданная процентная ставка останется без изменений, можно определить, какую сумму необходимо откладывать каждый месяц. Если аргумент "бс" опущен, необходимо использовать аргумент "плт".
тип – необязательный. Число 0 или 1, обозначающее, когда должна производиться выплата.
Для условия нашей задачи применение данной функции позволяет получить ответ на вопрос: «Какую сумму необходимо вложить в банк на депозит, чтобы получить через 5 лет величину вклада 26855,95 тыс. руб. при ежегодном пополнении вклада на 1000 тыс. руб., если годовая банковская ставка составляет 15%?».
Формула для определения текущей (настоящей) стоимости вклада (ПС):
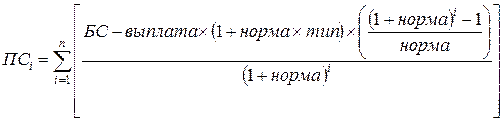 ,
,
Для нашего примера синтаксис функции будет следующим:
=ПС(0,15;5;-1000;26855,95)(Возвращаемый результат: -10000).
В случае, если периодичность выплат (поступлений) отлична от годовой, для любой из рассмотренных функций в данном разделе достаточно скорректировать соответствующим образом аргументы норма,ичисло периодов(i).
Допустим, при ежеквартальном пополнении вклада и начисления процентов, функция ПС( ) примет следующий вид:
=ПС(0,15/4;5*4;-1000;26855,95)(Возвращаемый результат: 1035,09).
Дата добавления: 2014-11-13; просмотров: 374; Мы поможем в написании вашей работы!; Нарушение авторских прав |