
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
КИНЕМАТИКА. Кеңістікте қозғалыстағы немесе тыныштық күйдегі денелердің орнын анықтауда таңдап алынған
Кеңістікте қозғалыстағы немесе тыныштық күйдегі денелердің орнын анықтауда таңдап алынған салыстыру денесі санақ денесідеп аталады.
|
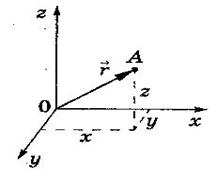
1-сурет
Материалдық нүктенің орны координаттардың декарттық жүйесінде x, y, z координаттармен немесе 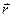 радиус-вектормен анықталады (1-сурет):
радиус-вектормен анықталады (1-сурет): 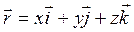
Қозғалыстағы материалдық нүктенің координаттары уақыт өтуімен өзгеріп отырады. Жалпы жағдайда, нүктенің қозғалысы
x=x(t), y=y(t), z=z(t), (1)
скалярлық теңдеулер жүйесімен, немесе оған балама
 (2)
(2)
векторлық теңдеумен анықталады. (1) және (2) теңдеулер материалдық
нүкте қозғалысының кинематикалық теңдеуі деп аталады.
|
|
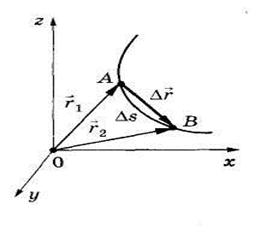
2-сурет
Нүктенің берілген уақыт сәтіндегі қозғалыс шапшаңдығы мен бағыты жылдамдықпенсипатталады. Материалдық нүктенің радиус–векторы өсімшесінің 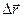 осы өзгеріс болған
осы өзгеріс болған  уақыт аралығына қатынасы орташа жылдамдық деп аталады:
уақыт аралығына қатынасы орташа жылдамдық деп аталады: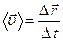 (3)
(3)
|
 |
3-сурет
Лездік жылдамдықтың модулі жолдың уақыт бойынша алынған бірінші туындысымен анықталады:
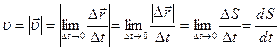 (5)
(5)
Айнымалы қозғалыстағы дене жылдамдығының модулі мен бағыты-ның қаншалықты тез өзгеретінін сипаттайтын шама – үдеу.Жылдамдық өзгерісінің сол өзгеріс болған уақыт аралығына қатынасымен анықталатын векторлық шама орташа үдеудеп аталады:
 (6)
(6)
|
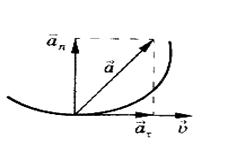 |
Материалдық нүктенің берілген t уақыт мезетіндегі лездік үдеуі орташа үдеудің шегіне тең:
 (7)
(7)
4-сурет
толық үдеуі тангенциал және үдеуі нормаль үдеулердің геометриялық қосындысына тең:

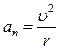
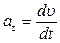 (8)
(8)
Материалдық нүктенің t1 -ден t2-ге дейінгі уақыт аралығында жүрген жолын анықтау үшін  функциясын білу керек:
функциясын білу керек:
 (9)
(9)
Бірқалыпты қозғалған нүктенің t уақытта жүрген жолы:
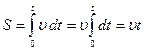
Бірқалыпты үдемелі қозғалған нүктенің t уақытта жүрген жолы:
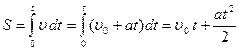
|
 |
Материалдық нүктенің қозғалмайтын оське қатысты радиусы R шеңбер бойымен айналмалы қозғалысында (5-сурет) бұрыштық орын
5-сурет
 |
уақыт бойынша бірінші туындысына тең векторлық шама:
|
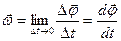 . (10)
. (10)
6-сурет
Нүктенің сызықтық және бұрыштық жылдамдықтары векторларының арасындағы байланыс:
 . (12)
. (12)
|
 |
7-сурет 8-cурет
Қозғалмайтын айналу осі маңайында айналып тұрған нүктенің орнын ось бойындағы кез келген О нүктесіне қатысты 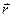 радиус-вектормен анықтағанда (7-cурет), оның сызықтық жылдамдығының модулі:
радиус-вектормен анықтағанда (7-cурет), оның сызықтық жылдамдығының модулі:

Бұрыштық үдеу бұрыштық жылдамдықтың уақыт бойынша бірінші туындысына тең векторлық шама: 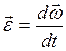 (13)
(13)
Үдемелі айналмалы қозғалыста бұрыштық үдеу векторы 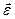 бұрыштық
бұрыштық
жылдамдық  векторымен бағыттас, кемімелі қозғалыста оған қарама-қарсы болады (8-сурет).
векторымен бағыттас, кемімелі қозғалыста оған қарама-қарсы болады (8-сурет).
Сызықтық және бұрыштық шамалар арасындағы байланыс:
 ;
;  . (14)
. (14)
 ;
;  . (15)
. (15)
Мұндағы:
 шеңбер радиусы;
шеңбер радиусы;  сызықтық жылдамдық;
сызықтық жылдамдық;  тангенциал үдеу;
тангенциал үдеу; 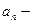 нормаль үдеу;
нормаль үдеу; 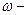 бұрыштық жылдамдық.
бұрыштық жылдамдық.
Дата добавления: 2014-10-31; просмотров: 1583; Мы поможем в написании вашей работы!; Нарушение авторских прав |
 уақыт арасында жүрген жолы
уақыт арасында жүрген жолы 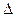 s деп аталады. Жол – уақыт-тың скаляр функциясы:
s деп аталады. Жол – уақыт-тың скаляр функциясы:
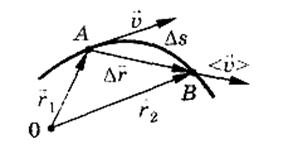
 Қозғалыстағы нүктенің бастапқы орнынан берілген уақыт сәтіндегі орнына жүргізілген
Қозғалыстағы нүктенің бастапқы орнынан берілген уақыт сәтіндегі орнына жүргізілген  вектор орын ауыстыру деп аталады (2-сурет). Түзу сызықты қозғалыста орын ауыстыру векторы траек-торияның сәйкес бөлігіне сай келеді, модулі нүктенің жүрген жолына тең:
вектор орын ауыстыру деп аталады (2-сурет). Түзу сызықты қозғалыста орын ауыстыру векторы траек-торияның сәйкес бөлігіне сай келеді, модулі нүктенің жүрген жолына тең:
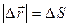 .
.
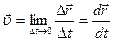 (4)
(4)
 дене жылдамдығының модулінің өзгерісін (бағыты траекторияға жанама бойымен), ал нормаль құраушысы
дене жылдамдығының модулінің өзгерісін (бағыты траекторияға жанама бойымен), ал нормаль құраушысы  жылдамдықтың бағыты бойынша өзгерісін сипаттайды (бағыты траекторияның қисықтық центріне қарай).
Қисық сызықты қозғалыстағы нүктенің
жылдамдықтың бағыты бойынша өзгерісін сипаттайды (бағыты траекторияның қисықтық центріне қарай).
Қисық сызықты қозғалыстағы нүктенің
 бұрылулар (шексіз өте аз) векторы ретінде қарастырылады. Осы вектордың модулі радиустың бұрылу бұрышына тең, ал бағыты нүктенің айналуына сәйкес бұралатын бұранда ұшының ілгеріле-мелі қозғалыс бағытымен (оң бұранда ережесібойынша)анықталады.
Айналыстың бұрыштық жылдамдығы
бұрыштық
бұрылулар (шексіз өте аз) векторы ретінде қарастырылады. Осы вектордың модулі радиустың бұрылу бұрышына тең, ал бағыты нүктенің айналуына сәйкес бұралатын бұранда ұшының ілгеріле-мелі қозғалыс бағытымен (оң бұранда ережесібойынша)анықталады.
Айналыстың бұрыштық жылдамдығы
бұрыштық  (11)
(11)
